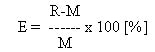Megfigyelések
Szerkesztések
Külső feladatok
Kurzusok
Tanulmányok
¤ Phd - Disszertáció
¤ Új Magyar Építőművészet-beli cikk (1998)
¤ "Utcarajzok szerkezeti felépítése" (2oo2)
¤ "Fulbright-ösztöndíjjal Amerikában" (2oo2)
¤ "Tónus a vonal mentén - a Helyi Kontraszt"
¤ Káoszból rend
¤ Küszöbszintek
|
|
| |
PhD - DISSZERTÁCIÓ
AZ ÉPÍTÉSZETI SZABADKÉZI RAJZ
SZERKEZETI FELÉPÍTÉSÉNEK OKTATÁSA -
ÚJ MÓDSZERTANI MEGKÖZELÍTÉSBEN
|
|
|
|
|
T A R T A L O M J E G Y Z É K |
| |
1. BEVEZETÉS - CÉLKITŰZÉSEIM
1.1. Választott témám háromoldalú körülhatárolása
1.2. Aránymérés és Rajzolási Sorrend - a KÉPES KOCKATAN tükrében
2. MÓDSZERTANI KÍSÉRLETEIM
2.1. A vonal-perspektíva alapelemeinek oktatása - redukciós módszerekkel
2.1.1. Az ábrázolandó környezet tancélú leegyszerűsítése
2.1.2. Térábrázolási módszerek összevetése
2.1.3. A távlati kép lebontása tisztavonal-hálóig
2.1.4. Redukciós lépések a rajzolás gyakorlati folyamatában
2.2. A "ferde" vonalak dőlés-mérése
2.2.1. A képsík-beli ferde vonalak oktatásáról
2.2.2. Dőlés-mérés hagyományos módon
2.2.3. Új megközelítések
2.3. Kísérleteim az "arányméréses" eljárás témakörében
2.3.1. Első kísérletek a "háromágú demonstrációs eszközzel"
2.3.2. Egy kísérleti óra levezetése
2.3.3. Eltérések számszerűsítése
2.3.4. Az "egyágú aránymérő" bevezetése
2.3.5. Több egyágú aránymérő egyidejű használatáról
2.3.6. "Képsík-keretes" aránymérés módszere
2.3.7. Háromféle segédeszköz összehasonlítása
2.3.8. A mérő-képsík beállításának jelentősége
2.3.9. A továbbfejlesztés lehetőségei
3. KÖVETKEZTETÉSEK - ÖSSZEFOGLALÁS - TÉZISEK
Kulcs-szavak gyűjteménye
Irodalomjegyzék
Függelék: Feljegyzések kísérleteimről
MELLÉKLETEK: I. Az "aránymérő" módszertani segédeszköz műleírása
II. Egy belső tér analitikus megközelítése ("Duna Plaza") |
|
1. BEVEZETÉS - CÉLKITŰZÉSEIM
1.1 A VÁLASZTOTT TÉMA HÁROMOLDALÚ KÖRÜLHATÁROLÁSA |
| |
Az Építészeti Szabadkézi Rajzoktatás keretén belül, a vonal-perspektíva alap-jelenségeinek ábrázolását tanító, új módszerekkel - közelebbről a ferdének látszó vonalak helyzetének pontos meghatározásával foglalkozom értekezésemben. Ehhez a problémakörhöz három irányból jutottam el.
Egyik út a városképi jelről (9) írt disszertációmat kísérő rajzok belső monológján keresztül vezetett, miközben a vonalas távlati kép szerkezeti felépítésének lépéseit elemeztem. A rajzolási sorrendről szóló fejezet a városképi jel és a szabadkézi rajz kapcsolatát tárgyalta. Itt fogalmaztam meg azt a felismerést, hogy jeltől-jelig araszolva, a részletek összeillesztésével készül a távlati rajz. A térbeli alakzatok képét síkvetületi elemekből állítom össze, a rész-idomokat a részletek közei kapcsolják egybe.
A rajzolási folyamat mely lépéseinél végeztem valóságos képsík-beli "aránymérést"?
Egyrészt a képsíkon megjelenő jellegzetes ferdék dőlésének bemérésénél (pl. a kiemelt pontra fektetett érintők, a negatív foltok peremei, a domborzat íveit helyettesítő húrok), másrészt a bevetítéseknél (pl. magasság-különbségek megállapítása, a vízszintesen mért távolságok függőleges skálához való viszonyítá-sa, stb.).
Mindegyik felsorolt fogás visszavezet a szabadkézi rajzoktatás kezdetéig - azaz a "kockológiában" elsajátítandó alap-méréseket alkalmazzuk - tudatosan vagy ösztönösen - a távlatrajzban.
A másik út eredete "A Szögletes Testek Rajzoktatásáról" (8) írt dolgozatom képsorában fedezhető fel, amikor a vonal-perspektíva alap-jelenségeinek ábrázolását képsík-felbontással közelítem meg.
A harmadik utat eddigi képzőművészeti munkásságom igazolja, hiszen a tiszta vonallal való rajzolás grafikus alkatomból ered. A VONAL - mint a távlat-kifejezés leggazdaságosabb módja - a távlatrajz szerkezeti felépítésének oktatása során önmagában is a kísérletezés tárgya és eszköze. |
|
| 1.2 AZ "ARÁNYMÉRÉS" ÉS A RAJZOLÁSI SORREND - A KÉPES KOCKATAN TÜKRÉBEN |
| |
Ebben a fejezetben pedagógiai tanulmányom (8) kritikai átdolgozását kívánom az értekezéshez csatolni.
Az újra-szerkesztés során felhasználom az első megfogalmazás óta összegyűjtött oktatási tapasztalataimat és beleépítem a tanítványok visszajelzéseit is - különös tekintettel az évről-évre visszatérő, általános típus-hibák orvoslására alkalmas, azok kialakulását valóban megelőzni képes módszertani lépésekre.
Az elsőéves építész- és mérnökkari hallgatók, valamint a felvételi előkészítőre járó középiskolások közül sokan a Rajzi Tanszék termeiben kerülnek először szembe a beállítás utáni rajzolással. A térbeli négyzetháló távlati ábrázolásában elkövetett leggyakoribb hiba a rálátások-alálátások torzulásának alábecsülése. A tanítványok nem akarják tudomásul venni a trapézzá torzuló alap-négyzetek zsugorodó magasságát. Az oktatás kezdeti időszakának fő célkitűzése e téves beidegződések kijavítására irányul.
Az építész beszéde a rajz. Nem hiszem, hogy a számítógép valaha is helyettesítheti az alkotó fantázia által vezetett "szabad" kezet!
A szabadkézi rajz szükségességének magyarázatához elég egy fénykép és az azonos szögből készült építész-jellegű rajz párhuzamos bemutatása. A különbség szembeötlő: csak a rajz képes a lényeg kiemelésére.
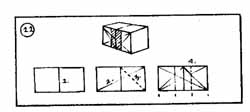
A kezdet-kezdetén egy végsőkig leegyszerűsített, váz-testet választunk a megfigyelés türelmes tárgyául, hogy a térhálóra redukált környezet modulján a perspektivikus alap-jelenségeket szemléletesen taníthassuk - hiszen a kockában a térbeliség három főiránya magától értetődő szabatossággal testesül meg.
A kezdőknek szükségük van a Tanszék hagyományos váz-kockáira. A modelltestek rajzoltatásával egy sor alapösszefüggés felismertetése, a "rajzolási sorrend" beidegzése a célunk. Így tanítjuk a megfigyelés tudományát: mit nézzünk, hogyan nézzük? Megmagyarázunk néhány elméleti fogalmat (pl. vetítés, képsík, rövidülés-összetartás, iránypont stb.). Bevezetünk néhány technikai fogást is (pl. szakaszok összevetése, "aránymérés", rajztábla-peremek és a ceruza mérőeszközként való használatát, stb.). Amit egyszer a diák a kockán megtanult, azt később bármilyen természet utáni ill. intuitív rajzfeladatnál alkalmazni képes.
Vegyük pl. a vízszintes irányú bevetítés fogását, amellyel a térháló-sarkok alapvonaltól való látszólagos magassági helyzetét tisztázzuk! Ilyenkor a legközelebbi kocka-él a függőleges skálánk. A bevetítés eleinte a rajztábla felső élével történik. Később megelégszünk a szabadkézzel meghúzott szerkesztő vonalakkal is. Gyakorlottabb korunkban, a levegőben mozgatjuk a ceruzánkat, végül csak szemmel végezzük az ilyenfajta ellenőrzést. Ezek a lépések a távlatrajz szerkezetének tudatos felépítéséhez tartoznak.
Jobb oktatási eredmény eléréséhez hatékonyabb módszereket kell alkalmaznunk.
A hagyományos szabadkézi rajzoktatásban jól bevált, hogy egymással összhangban lévő, csereszabatos, váz-szerkezetű illetve "tömör" alap-idomsorral dolgozunk, melyhez egyéb kellékek is járulnak. Elsősorban a színes négyzetlapok fontosak, melyeket az alapsíkok tagolására használunk. A méréseket a határoló térsíkokra rajzolt négyzetháló nagyon megkönnyíti. A szemsík berajzolása a falakon lévő vízszintes osztás-sor segítségével válik nyilvánvalóvá. Állítható élű nagykocka modellként való alkalmazása is eredményes szemléltető eszközünk. A mércén bizonyítható a rajzi tévedések mértéke.
Ez volt az első gondolatom a tér felnagyított kocka-belsőként való ábrázolására - így merült fel valamilyen kézzelfogható eszköz keresésének az igénye, hogy a szóbeli kritikán túlmenően demonstrálhassam a képsíkbeli tévedéseket
További hasznos segédeszközeink a tükrök és a függönyök. Így pl. változtatható síkú, görgős állványra szerelt nagy síktükröket ellenőrzésre ill. a beállítás megsokszorozására lehet használni. A függönyök a vázszerkezet eltakarása révén alkalmasak a takarásos perspektíva "vonalhiányos" jelenségének bevezetésére.
A jelen eszköze a nálunk ritkán használt írásvetítő. Egyaránt alkalmas a fólialapon filctollal a helyszínen fejlesztett folyamatábrák, vagy az előre elkészített ("kitakarásos-ablakos") ábrasorok bemutatására. A táblarajzzal ellentétben, ezeket a lapokat meg lehet őrizni. A diákok jobban elfogadják a mintákat, ha folyamatában végigkövetik a szemük láttára felépülő megoldást.
A rajz több, mint a tárgy másolása. A tanítvány hibásan rajzolja a látványt, ha a benne lévő összefüggéseket nem érti. |
| |
| |
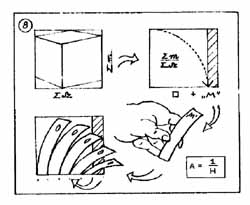
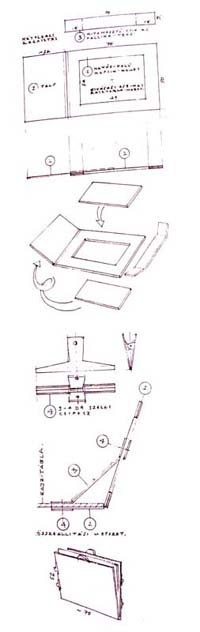
A "KÉPES KOCKATAN" részei:
I. ELŐKÉSZÜLETEK: Beállítás, képkivágás, elhelyezkedés. A látvány és a rajzoló viszonya. Főirányok, oldaltávolságok.
II. AZ ALAPVONAL-HÁLÓ SZERKEZETI FELÉPÍTÉSE: A rajzfelület részekre bontása: a lényeges metszéspontok rögzítése, "aránymérések". A főirányok és a "ferdék" viszonya; vetítések, negatív formák, a szemsík kikeresése. A vonal- perspektíva alap-jelenségeinek magyarázata.
III. ELLENŐRZÉS: Függőlegesek, összetartások. Kiegészítő szerkesztések.
A rajz továbbfejlesztése ezután egyéb távlat-kifejező eszközeinkkel - az alapvonal-háló "felöltöztetésével" folytatódik. |
|
I. rész: ELŐKÉSZÜLETEK
|
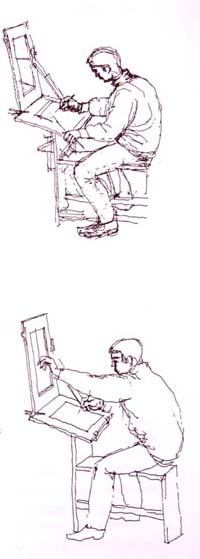
A bevezető képsor a látvány és a rajzoló viszonyával foglalkozik. Hogyan kell leülni, a rajztáblát tartani, a rajzlapot felerősíteni?
Már az oktatás kezdetén szükséges a beállítás tárgyához annak környezetét is hozzárendelni. A hallgatók jellegzetes típushibája ugyanis az, hogy rajzukon darabonként "ragasztják" egymáshoz a tárgyakat: az oldaltávolságok (tárgy-közök) figyelembe vétele nélkül! A tárgy-kontúrba való háttér-belemetsződéseket is csak utólagos felszólításra hajlandók felismerni. Ebben a fázisban tervezzük meg a "téma- és rajzfelület" együttesének sík-kompozícióját.
|
|
1. A távlati kép a tárgyból - mint főtémából - és környezetéből tevődik össze.
|
|
A nézőpontot úgy kell kiválasztani, hogy a témát (a tárgyat és környezetét) zavartalanul láthassuk. A függőleges élek lehetőleg ne essenek egybe! Már a leülésnél komponálunk - megfelelő nézési irány és szemmagasság kiválasztásával.
"Értsük meg az egész formát, ha szükséges, annak körbe-járásával - hiszen egyszerre csak egy nézetnyi látszik belőle." (10)
Itt az alkalom a képsík, a vetítő-sugár (a vetítés) fogalmainak bevezetésére.
|
|
|
2. Gondosan keressük ki a megfelelő nézőpontot (a nézési irányt és a szemsíkot) - akár a beállítás megkerülésével. |
|
|
|
3. Az egész fő-témát lássuk, ne hagyjuk fontos részeit eltakarni. A rajzlapot szilárd alaphoz, biztonságosan rögzítsük. A rajz (ill. rajztábla) derékszögű széleit zavartalanul követhesse tekintetünk a rajzolás teljes folyamatában, mivel a szemnek biztos főirány-támaszokra, saját koordináta-rendszerre van szüksége a rajzon belül. |
|
|
|
4. A "felező-sík" kikeresése - a képsíkok szemléltetése. A rajzoló "felező-síkjával" célozza meg a téma középpontját. |
|
|
|
5. A rajzbeli főirányok bemutatása. A rajztábla peremének kisujjunkkal való követése.
|
|
|
A függőlegesek a rajztábla-rajzlap függőleges oldalaival lesznek párhuzamosak. Ezt az oldaltávolságot időről-időre mérjük le: ez hagyományosan a "ceruza-csúsztatással" történik. (Erre az "aránymérő" ága is befogható!) A táblaperemtől mért oldaltávolságot (0r) a főirány-beli vonal mentén kísérjük végig. Túlzott vonalvastagság, merev kéztartás, azaz "vésés" ellen is használhatjuk a kisujjra való kéz-letámasztás módszerét. Egyébként a szemünkkel követjük a rajztábla széleit; csak a két főirány a biztos!!
|
| "A látvány utáni rajzolásnál a papír széleit használjuk szögmeghatározásra". (3) |
| |
|
6. Az oldaltávolságok magyarázata - a főirányok ellenőrzése. |
|
|
II. rész: A TÁVLATRAJZ SZERKEZETÉNEK FELÉPÍTÉSE: AZ ALAPVONAL-HÁLÓ KIALAKÍTÁSA
|
Már az első vázlatnál szükséges egyidejűleg figyelembe vennünk a főtéma befogadó formáját és környezetét is ahhoz, hogy a rajzlap felületét megfelelően beoszthassuk.
Ez leegyszerűsítve annyit jelent, hogy a környezetet helyettesítő alap-síkok metszésvonalait "pókhálóként" feszítjük ki a főtéma foltja és a rajzlap szélei között, gondosan mérlegelve az így kialakuló mezők arányát.
|
|
7. A rajzfelület tagolása: előtér, háttér és az oldalmezők. A befoglaló forma és a "negatív formák" keletkezése. |
|
|
Ilyen belemetsződéseket figyelhetünk meg a tárgy/kontúr és a fal/padló sarok-élei között. További felület-osztások is minket segítenek.
A tárgy pontjainak egymáshoz való viszonyát a diák általában hamarább tudja ábrázolni, mint a tárgy és a környezete között kifejezendő térhatást. A "csupasz kocka" még csak részleges, kontúron belüli részhatást eredményez - összetett mélységérzetet a tárgy szélső pontjainak a külső környezetéhez viszonyított helyzet-érzékeltetése kelt. Ragaszkodjunk ahhoz, hogy ne csak a beállított tárgy, hanem annak (sematikus) környezete is szerepeljen a rajzon!
A negatív foltok és a főméretek fogalmával először a "befoglaló formánál" találkozunk, amikor a beállítás szélső pontjaira ráillesztjük a főirányokat.
Mivel a környezethez való tárgy-viszonyítást valamilyen rendszer szerint célszerű gyakoroltatni, a térbeli ábrázoláson túl vetületekben is dolgozzuk fel a beállítást. Használjuk ki a határoló térfalak és felületek osztásrendjét! Egységnyi négyzetlapok révén már az oktatás elején hidat építhetünk tárgy- és tér-ábrázolás között.
A párhuzamos és a centrális vetítés elméletének bevezetése megkönnyíti az oktató dolgát. Ettől kezdve a vonalperspektíva bizonyos jelenségei egyszerű nézetekben is körülírhatók. |
|
|
8. Az első aránymérés, a főméretek viszonya. ("Hogyan mérlegeljük két szakasz arányát?" Az egész és a maradék viszonya, a legnagyobb közös osztó megállapítása.) |
|
|
A méréseket aránypárként visszük át a rajzunkra, ehhez azokat számszerűsíteni kell. Ez azt jelenti, hogy a szabadon választott, rajzbeli méret (SR) és a mérő-képsíkon megfigyelt, látványbeli társa (SM-Ks) közti eredeti arány szerint dolgozzuk fel megfigyeléseinket.
|
|
9. A belső összmagasság szétbontása - (váz-kocka esetében: alsó, középső és felső részekre. Betűkkel jelölve: A + K + F = SM). |
|
|
A főméretek összevetése után a belső osztást vesszük szemügyre: az összmagasság három részből tevődik össze. Az alsó, a középső és a felső mező csíkja eltérő grafikával jól elkülöníthető. Ide tartozik a belső élek függőleges vetítéssel történő meghosszabbítása is. (Padló-tükröződés vagy kocka-torony esetén ezek a függőlegesek valóban látszanak.) Most tudjuk az összmagasságra a rész-szakaszokat kivetíteni. Mivel a csík szélessége egységnyi, a foltok területe helyett elég azok magasságát hasonlítjuk össze. ("Hányszor fér a foltok magasságába az egységnyi szélesség?") Az arány tisztázása érdekében köröket (esetleg rombuszokat) rajzolunk a csíkokba. Ez egyúttal a felső lap rálátását és a hátsó (IV.) él helyét is véglegesíti.
|
|
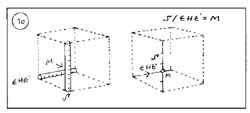
10. A belső mag tagolásával egyidejűleg határozzuk meg a közeli függőleges él (S) és az (alap)-Egység Hátsó Élének (EHÉ) látszólagos egybeesésének metszéspontját (M). Ez a modulkocka szerkezeti felépítésének talán a legfontosabb lépése. Képletben: S/EHÉ = M. |
|
|
Az (M) jelű metszéspont felismerése - amely az összmagasság belső tagolásának is része - egyértelműen rögzíti az alsó négyzetlap látszólagos torzulását.
|
|
11. A rajz-felület tagolása; azaz a téma belső és külső (pozitív és negatív) részeinek - az "aránymérés" szempontjából jól használható - egyszerű mértani formákra való bontása. A kontúr és a környezet összemetsződéseinek megfigyelése. |
|
|
Külön ábrasor követi végig az eddig alkalmazott, hagyományos mérő-módszert : a nyújtott karral kitartott, ökölbe-szorított ceruza, amelyen a hüvelyk-ujjunk volt a "csúszó"-végpont, miközben igyekezni kellett ceruzánkat a kartávolságban elképzelt képsík-alkotó üveglap felületén mozgatni. A két mozdulat neve: vízszintes bevetítés (Y/S), illetve negyedköríves vetület-összehasonlítás (X/S).
|
|
| |
| 12-13. A "ferde-mérés" hagyományos módszere: a rajztábla-perem vízszintes vetítő-vonalként való megemelése a talp-pontig (0), illetve a keresett sarokpontig (B). Az Y/S arány meghatározása három lépésben (I-II-III).
|
Az alapvonal-képzés mozdulata - a rajztábla felső peremét a szemsíkkal párhuzamosan tartva csúsztatjuk. A mozdulatot kísérő oldalnézetekkel teszem egyértelművé. Fordítsunk elegendő időt a legmeredekebb (a legszélső) "ferde" szakasz dőlés-mérésének gondos részletezésére!
|
|
14. A hagyományos "ferde-mérés" második lépése: a "ceruzás"-módszer mozdulatai.
Az X/S arány meghatározása a képzeletbeli képsíkon, ceruzás szakasz-befogással, s az azt követő negyed-köríves összehasonlítással. Ez a piktogram eddigi tanári pályafutásom leghatékonyabb ábrájának bizonyult. |
|
|
|
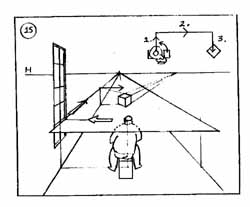
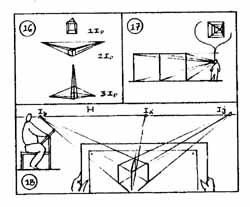
15. A rajzoló szemsíkjának meghatározása. A képen filmszerűen követhető a hátulról bemutatott figura, amint fejével metszi a horizont síkját. Ezen a vízszintesen kifeszített "vásznon" nyilakkal kísérem az oldalra pillantás fejfordulatát, ahogy a rajzoló a téma fölé kíséri az oldalfalon beazonosított szemsíkot.
A végtelen horizontot (H) lehatárolt peremmel ábrázolva jobban érzékeljük. Ezért a magyarázó rajzon a tér a "folyosó" faláig tart. |
|
|
|
16-17-18. A perspektíva alap-jelenségeinek térbeli alapvonal-hálón bemutatott magyarázata. (Képsík, vetítősugár és a szem, mint központ; a horizont és az iránypontok, ill. az átlók iránypontjai; a perspektíva hétköznapi esetei). |
|
|
I. rész: ELLENŐRZÉSEK
|
|
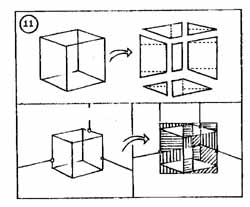
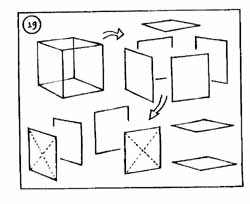
19. Kocka-ellenőrzési módszerek: képzeletben, egyenként (széthúzva ill. párosával összevetve) vizsgáljuk a kocka határoló síkjait. Egy-egy lap ellenőrzésénél próbáljunk a többi oldal látványától ideiglenesen elvonatkoztatni és átlókat képezni. |
|
|
|
|
20. Ellenőrzés-szerkesztéssel: az "átlós módszer". Négyzetoldal, ill. szakasz szaporítása sarok-tükrözéssel.
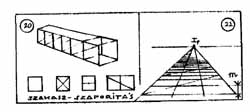
21. A térhatároló felületek alapvonal-hálója (a felületosztás ill. anyagjelölés születése); a "padló-háló" kiterjesztése átlós szerkesztéssel. (Az előtérből hátrafelé haladjunk!). Első dolgunk a legközelebbi négyzetsor magasságának megbecsülése (m) legyen. |
|
|
|
22. A harmadoló módszer lépései. Egy kettős-négyzetnyi téglalap négyzet-elemeinek átlói ill. a téglalap saját átlói egymást - a két négyzet-oldalnyi szakasz viszonylatában - harmad-pontokban metszik. |
|
|
|
23. Az összetartások és a függőlegesek ellenőrzése - utólagos rajztábla-mozgatásokkal történik. Munka közben időnként álljunk felés friss szemmel, távolabbról nézzük meg rajzunkat! |
|
|
|
24. A függőlegesek bizonytalanságát a fejjel lefelé fordított rajz deríti ki. Az elfáradás miatt saját hibáinkat hamar megszokjuk: alkalmazzunk tükröt, vagy a rajzlapon való átnézés módszerét! |
|
|
Látható, hogy a fejezet döntő része a ferdék felismeréséről, dőlés-helyzetük pontos megítéléséről szól. Ez az a rész-probléma, amely köré értekezésem főtémája, az "aránymérés" módszere kristályosul. |
|
| 2. MÓDSZERTANI KÍSÉRLETEIM |
| |
Kísérleteimet a Budapesti Műszaki Egyetem Rajzi és Formaismereti Tanszékén, a szabadkézi rajzoktatás bevezető szakaszában, magyar és idegen nyelvű, építész- ill. építőmérnök-hallgatók körében végeztem az 1996-97 tanévben. Újszerű módszertani megközelítésemet 1997 tavaszán kipróbálhattam a Ecole d'Architecture de Strasbourg (Franciaország) DEFA I/II / C1 évfolyamán is. |
|
| 2.1 A VONALPERSPEKTÍVA ALAPELEMEINEK OKTATÁSA - REDUKCIÓS MÓDSZEREKKEL |
| |
| A FERDE-VONAL FONTOSSÁGA |
| |
Mottó: A rajztudás nem más, mint térábrázolás képessége sík-felületen . (= TÉR - ÁBRÁZOLÁSA - SÍKBAN) |
|
| |
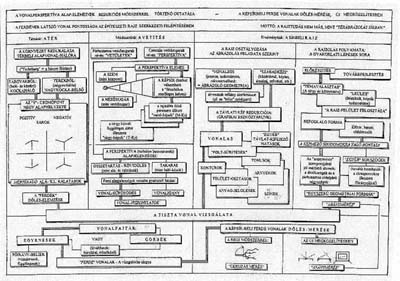
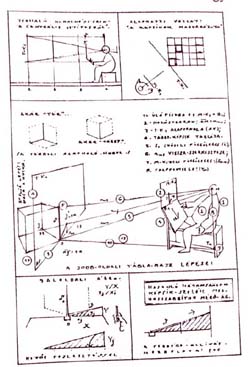
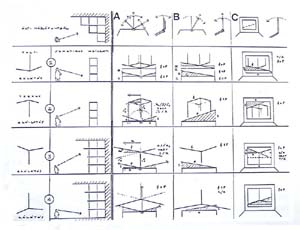
Minden szónak a mellékelt áttekintés egy-egy oszlopa felel meg. Ezzel a négyoszlopos táblázattal kívánom a "ferdék" fontosságát bizonyítani és az "arányméréses" megközelítést körülírni.
Kitűzött oktatási célunk, hogy a diákok elérjék az építészeti szabadkézi rajztudás látványtervi szintjét. A tanítványok adottságaira építve, azok szemmértékét, arányérzékét is fejlesztjük - gyakorlati készségüket, technikai eszköztárukat bővítjük, miközben rajzolási sorrendet is tanítunk.
A képsík-beli "ferdékhez" a tiszta-vonalon keresztül vezet az út. |
| |
| |
| "TÉMÁNK: A TÉR. MÓDSZERÜNK: A VETÍTÉS. EREDMÉNYÜNK: A SÍKBELI RAJZ." |
| |
Ebben a sorrendben követik a táblázat oszlopai a fejléc jelszavát. Az oszlopokat felülről kísérem lefelé, hogyan torkollanak bele a táblázat közös alsó sávjába, ahol a tiszta-vonalakat vizsgálom. |
| |
| |
| 2.1.1. A KÖRNYEZET REDUKCIÓJA |
| |
Az első oszlop tartalmazza az ábrázolás tárgyát: ez a TÉR. A "tér" fogalmába teljes környezetünket beleértem - ezt bontom tovább kisebb tárgyak halmazára, amiből a nagyobb tömegek újra felépülnek. A következő lépésben térhatároló elemekkel kerí-tem el saját (épített) tereinket a végtelentől.
A tér-ábrázoláshoz határoló-síkok és tárgyak szükségesek. A mélység-érzékeltető térsík-határt (a tárgyakon túlmenően) felület-osztás is kifejezi.
A térfalakat függőleges és vízszintes síkokra redukálom. A tárgyakat befoglaló for-máikkal váltom fel. A görbe felületeket burkoló síklapok, az íveket húrok vagy érin-tők képviselik.
Az oktatás szempontjából környezetünk alkotó részeit egyszerűsített térbeli alapvonal-hálóra bontjuk. A tárgyakat kocka-sorokkal, a tereket négyzethálós nagykocka-belsővel helyettesítjük. A távlatrajz szempontjából a mélység érzékeltetése a kriti-kus.
A fent leírt alap-síkokká redukált környezet, ill. a főirányokkal párhuzamos síkok révén "becsomagolt", majd egységnyi kocka-elemeire bontott "tárgyi" világ alap-vonalhálójának helyes ábrázolása kitűzött oktatási cél-feladatunk - ebben a kezdeti fázisban.
A távlat-rajzban először azt tanítsuk meg, hogyan lehet ábrázolni az alap-síkok négyzethálóinak látszólagos torzulásait!
Az ábrázolás folyamatának következő szakaszára marad a belső váz-szerkezetre kí-vülre, vagy - azt külső állványzatként tekintve - belülre építendő "egyéb" részletek igazítása; az alaphálótól eltérő osztások, felületek és más formák kidolgozása.
A mértékadó (azaz a legnagyobb) rá- ill. alálátások vizsgálatát a fenti redukcióval nyert térbeli alapvonal-háló magjában, az ún. "Y-csomópontban" hajtom végre. A tárgy-kockát és a tér nagy-kockabelsőt legjellemzőbb alkotórészeire (pozitív és negatív sarkokra, alá- ill. rálátásokra) bontom. Így rendre 3-3 egyenes egy pontban való találkozási helyén az "ágak" ferdéinek a főirányokhoz való viszonyát vizsgálom.
Redukált tértől a tiszta-vonalig a "ferdék" dőlés-elemzése révén jutok el. |
| |
|
| |
He who has mastered these three lines, has practically mastered perspective.
("Az a mestere a távlatnak, aki e három főirányt uralja.")
R.G.HATTON |
| |
| |
| A kockarajzoltatás értelméről |
| |
Nem túlzás azt állítani, hogy a parallopipedon (téglaforma) és ezen belül - egyenlő élei miatt - a kocka a legmegfelelőbb kiindulás a távlati kép tanításának kezdetén.
Ökölszabályként kijelenthetjük, hogy a minket körülvevő valóság minden formája és tere felépíthető vagy lebontható ezekből. Lapjainak arányos továbbosztásával, illetve háromirányú megsokszorozásával, bármilyen tömeg- és tér-formációhoz eljutunk.
Ugyanez érvényes azokra a formákra, alakzatokra és terekre is, amiket még csak ezután fogunk kitalálni. Közelebbről: "Mindkét alakzat csak háromirányú, egymásra merőleges vonalakból áll és van olyan kezdőpont is, ahol ezek szétágaznak." (5)
Megjegyzés: nem szabad a tér három főirányát a képsík (ill. rajzsík-beli főirányokkal) összekevernünk. Saját koordináta-rendszerünk biztonságos kapaszkodói: a rajzlap-keret vízszintes és függőleges pereme (lásd 1.2.5.).
A kockák egység-modulok is, befoglaló-formák, a tárgyakból és terekből álló formarendünk mérő-edényei. Környezetünkben viszonyítási alapul szolgálnak - határoló síkjaik tér-érzékünk koordináta-rendszere. A magassági méreteket is "sarkokban felhalmozott kockákon át" közvetítve érzékeljük igazán.
Illusztrációképpen a minket körülvevő kocka-világra álljon itt a "Köri szobája" c. linómetszetem - átültetve kockák nyelvére is. |
| |
|
|
| 2.1.2. TÉRÁBRÁZOLÁSI MÓDSZEREK ÖSSZEVETÉSE |
| |
A táblázat második oszlopában a VETÍTÉS, mint általános tér-leképezési módszer szerepel, amely a Téma és az Eredmény közötti kapcsolatot biztosítja.
A vetítést a vetítő-sugarak iránya szerint osztályozom. E szerint a vetítés lehet párhuzamos - ez eredményezi a vetületeket; és lehet centrális - ez a mi perspektívánk. Az oszlop további része kettéoszlik - Először a perspektíva elemeit, majd alap-jelenségeit veszem sorra.
"Bár Kopernikusz óta (1543) elterjedt az a nézet, hogy bolygónk nem a világ köze-pe, a perspektivisták jóvoltából minden festmény, metszet, madártávlatból készített kert- ill. városkép azt sugallta, hogy a világmindenségnek a szemlélő a középpontja. Minden visszavezethető az emberre: minden leegyszerűsödik a retinánkon észlelhe-tő jelekig." (2)
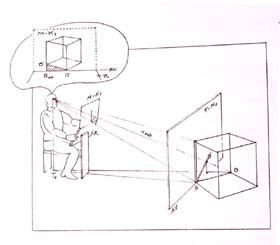
A centrális vetítéshez szemre (mint központra), vetítősugárra (nálunk inkább: "nézősugár") és képsíkra van szükség. Ez utóbbi címszót vizsgálom tovább: mivel a rajzoló a "felezősíkjára" merőleges - egymással párhuzamos - képsíkok közül szabadon választhat, gyakorlati szempontból a rajztáblája peremére állított mérő-képsík (M-Ks) lesz a döntő. Méréseit ezen tudja majd legpontosabban elvégezni. Ez a "megfigyelés" képsíkja.
"Alberti fátyol-elmélete szerint a kép egy olyan ablak, amelyen át a mozdulatlan szemlélő a külvilágot nézi." (13)
A perspektíva alap-jelenségeit az oszlop második felében tárgyalom. A címszó úgy kapcsolódik az első oszlophoz, hogy az alap-jelenségeket is redukált térháló segítségével mutatom be.
Legfontosabb alap-jelenségek elemzésem szempontjából: az összetartás-rövidülés (mint alá- és rálátások); továbbá a takarás - amint a háló-közök lapjait át-nem-látszóvá teszem. A fenti jelenségek vonalra gyakorolt hatását a következő címkék szemléltetik: az összetartás-rövidülés főleg vonalsűrűsödést, a takarás pedig vonalhiányt okoz.
Így jelennek meg ennek az oszlopnak az alján is a "vonal-viszonylatok". |
|
| A perspektíva alapjelenségeinek ösztönös megközelítése |
| |
Ha a magamfajta - művészettel is alkotó módon foglalkozó építész-tanár elmélyed a "vonalzós" távlattan tudományos elméletébe, hamar visszariad a bonyolult levezetések tömkelegétől, amelye-ken a munka-folyamat, azaz a szerkesztési sorrend nehezen követhető.
Mi, rajzosok, kevésbé ragaszkodunk a tudományos háttérhez. Inkább ösztönös megfigyeléseinkből, sok gyakorlással megszerzett tapasztalatainkból, híres előképek és minták tanulmányozásából élünk.
Ehhez a keverékhez adjunk hozzá egy kevés elméletet, benne néhány egyszerű szerkesztési és önellenőrzési módszert! Így közelíthetjük meg legjobban oktatási célkitűzéseinket - a két irányban vizuálisan kommunikálni képes építész-jelölt eredményes felkészítését. Választott témám nem kíván foglalkozni az Ábrázoló Geometria szakterületéhez tartozó bizonyítékokkal - a perspektíva tanulságos történetébe sem merülök el. (ld. 7)
Munkámmal az építész-képzés szabadkézi rajzzal kapcsolatos oktatási módszereinek továbbfejlesz-téséhez kívánok hozzájárulni. Meggyőződésem, hogy aki képes kívánság szerinti nézőpontból, - akár fejből is - kockát rajzolni, az valóban "uralja a távlatot". Véleményem szerint a kocka sarkai-ban összefutó három térbeli főirány helyes ábrázolása a szabadkézi rajztanítás alsó küszöb-szintje.
Tárgyunk neve: Építészeti Szabadkézi Rajz. A távlat látszatának szimulálását az ösztönös megfigyelés oldaláról közelítem meg. Elhatárolódom a szerkesztések "iránypont-fétisizmusától" - mivel az iránypontok túl gyakran esnek távol rajzfelületünktől - ezért inkább csak utólag ellenőriztetem az összetartást. Fő törekvésem a perspektívának, mint jelenségnek az érzékeltetése. |
|
| MI A PERSPEKTÍVA LÉNYEGE? "Illúzió, a térbeli mélység érzetének élménye." (14) |
| |
"A perspektíva olyan grafikus ábrázolásmód, amellyel a normális látás során keletkező képhez hasonló képét állítjuk elő valós vagy képzeletbeli tárgyaknak." (6)
"Gyakorolni a perspektívát - kétirányú művelet: láttatjuk, ami van és egyúttal azt is, ami volt, ill., amivé lehetne. Egyaránt szolgálja a képzeletet és az állapot-felmérést. Megmutatja a múltat, a jövőt és a jelent is." (2)
A távlati képnek az a feladata, hogy elhitesse a szemlélővel: a papír-sík vonalai (hála a ferdéknek!) "mélységet" jelenthetnek.
A vonalrajzra redukált képen a távlati mélységérzet kialakulásáért elsősorban a térhálóra redukált környezet párhuzamos éleinek összetartásai és a hálóközök rövidülései felelősek. Ezt a jelenséget a képsík-beli vonalak főirányokhoz viszonyított dőléseként érzékeljük. |
|
| 2.1.3. A TÁVLATI KÉP LEBONTÁSA A TISZTAVONAL-HÁLÓRA |
| |
A harmadik és negyedik út a tisztavonalas ferdék felé a SÍKBELI RAJZ-on át kereshető. A táblázat kettős oszlopa egyfelől az ábrázolás feladata szerint, másfelől a rajzolás gyakorlati oldalán keresztül közelíti meg az értekezés tárgyát.
A kitűzött ábrázolási cél szempontjából elkülönítem a tudományos, "vonalzós" ill. a képzőművészettel rokon "szabadkézi" rajzot. Az előbbi inkább az Ábrázoló Geometria területe. |
|
| A Szabadkézi Rajz és az Ábrázoló Geometria kapcsolata |
| |
A perspektivikus leképezési mód az Ábrázoló Geometria tudományterületének része - amelynek egy speciális " szabadkézi " fejezete a mi szakterületünk. Vizsgáljuk meg, melyek tárgyunk közös vonásai az Ábrázoló Geometriával; és miben különbözünk attól?
A választó-vonal az elnevezésben rejlik: az egyik "vonalzós", a másik "szabadkézi". Az Ábrázoló Geometria matematikai fontossággal foglalkozik a tárgyak és terek egyértelmű síkbeli ábrázolásával oly módon, hogy azok méreteit, egymástól való távolságát, térbeli szomszédságait meg lehessen határozni. (Ezt ők a "visszaépíthetőség feltételének" nevezik.)
A rekonstruálhatóság náluk gyakran a képiesség, a közérthetőség rovására megy. A laikusok számára a perspektíva jobban felfogható - ezért a látványterv a tervdokumentáció ki nem hagyható része.
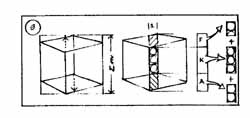
A pontosabb méretekről, az eltakart részekről és közökről, a távoli részletekről a kellő számban elkészítendő egyéb rajzok (nézetek, alaprajzok, metszetek, helyszínrajzok), révén kapunk és adunk információt, amelyek - a visszaállíthatóság - érdekében a párhuzamos vetítés módszerével készülő vetületek . (A vetületekhez általában a Monge-féle ábrázolási rendszert választjuk, amelyben a képsíkok egymásra merőlegesek. Ennek alapelvét a térsarokba állított kockával illusztráljuk: ahol az egység-kocka oldalai párhuzamosak a falakkal, valamint egységnyi a hát- illetve oldal-távolság is.)
Az egyértelmű térhatás érzékeltetéséhez tehát nem elég egyetlen távlati kép - hiszen a kép csak arra bizonyság, hogy az adott helyről nézve a tárgy, illetve a tér milyennek látszik .
Más szóval: a kép-pont is rajta van a tárgy pontját a vetítési központtal (a szemünkkel) összekötő vetítő-egyenesen. Milyen mélyen helyezkedik el a tárgypont a vetítő egyenesen? Ehhez további adatok kellenek! Az ábrázoló geometriában az egyéb vetületek válaszolnak erre.
Az elméleti bevezetés képsorában a tárgypont és a centrum távolságát oldalnézettel magyarázom (1.2.17.).
A következő lépésben a távlati kép vonalhoz vezető redukcióját végezzük el. Grafikai eszköztárunk kellékei két fő csoportra oszlanak: vonalas és "egyéb" távlat-kifejező eszközökre.
A vonalas rajz lehet tiszta vonalból álló kontúr-rajz - melyet felületosztásokkal és anyagjelölésekkel (ún. " folt-sűrítésekkel ") gazdagíthatunk. Ezek átmenetet képeznek a vonalrajz és a tónusrajz között. A tónusok csoportjába sorolom az árnyékolás és a színezés technikáját. Ennek az oszlopnak a végigkövetésével jutok el a harmadízben is tiszta vonalig .
A vonalháló meghatározó jelentőségű az építészeti szabadkézi rajz szerkezeti felépítésében. Az oktatásban a szélsőséges kivételektől (ilyenek, pl. a csupán elmosódó folt-hatásra épülő kísérletek) egyelőre eltekintek.
A rajztanítás nélkülözhetetlen állomása a vonal-tanítás.
"A vonal a rajzon ne csak azt jelentse, hogy egy tárgy milyen széles vagy milyen hosszú; erre ugyanolyan jó lenne a vonalzós rajz is. Az a fontos a vonalnál, hogy az a lehető legtöbbet elmondja arról, amit a tárgyról egyáltalán tudunk!" (10)
Elemezzük a vonalháló-rétegek optimális felépítésének a sorrendjét - mégpedig a távlatkeltést kifejező funkciójuk szerinti csoportosításban! Vonatkoztassunk el minden egyéb mélység-teremtő eszköztől, s haladjunk visszafelé a kész képtől az üres rajzlap felé! Először búcsúzzunk el a színektől, tónusoktól, részletektől, felületosztásoktól - csak a lényeget körülíró kontúrok maradnak. Legyen a kép csupa "tiszta-vonal"! Az utolsó előtti állomás - az érintetlen papír fehérje előtt - mindenképpen maga a tiszta vonalháló lesz, amelyben főleg a vonalak irányával és a szakaszok hosszával fejezzük ki a mélységet, továbbá vonalsűrűsödéssel és vonalhiánnyal dolgozunk (ld. 2.1.2.).
"Fehér grafikának" (graphisme blanc) nevezi a csak vonalból álló képet J.P.Jungmann, a vonal és a látványtervek kézikönyvében, amely az építészetet "optikai gépezetnek" tekinti, s a rajzilag elérhető effektusokat a különböző fényviszonyok, a távolság, az anyagok, a stílusok ill. az alkalmazott grafikai eszközök kölcsönhatás-mechanizmusa szerint csoportosítja. (7)
A térhatás illúzióját leggazdaságosabban - a lehető legkisebb ráfordítással; ha azt az adott idő alatt a megfelelő helyen húzott vonalak hosszával mérjük - a "tiszta-vonalak hálójával" érhetjük el.
Feladatunk e szerint már csak a "megfelelő helyek" megtalálása marad! Tanulmányomnak éppen ez a célja: ráirányítani az olvasó figyelmét a térmélységet leginkább kifejező vonalfajták - a ferdék - pontos "megfogásának" módszereire. |
|
| A Tisztavonal-Háló helye a Rajzolási Sorrendben |
| |
Azt kívánom bizonyítani, hogy a tisztavonal-háló első helyen áll, alapozó jelentőségű, a szerepe döntő - nélküle nincs kép; ha hibás, hiába minden további szépítő technika!
Vajon meddig tart a tisztavonal-rajz és melyik fázisban kezdődik a tónusrajz ?
Nyilvánvaló az átfedés a kétféle rajztípus között, pl. a "hátrafelé sűrűsödő" felület-osztás már árnyékolásnak hat. Fordított esetre is könnyű mintát találni; amikor az árnyék-hálót "felület-rovátkolásnak" nézzük. A grafikai kellékek csoportjai között a határ elmosódik.
Vegyük példának a mellékelt kőoszlop-rajzomat: (a spanyolországi Segovia római-kori vízvezetékének egyik tartópillérét ábrázolja.) |
|
A RAJZOLÁSI SORREND az alábbiak szerint alakul: |
|
|
|
1. Először készül a nagyobb tömeget a környezetétől elhatároló befoglaló körvonal - amely a kiterjedést fejezi ki.
|
|
|
2. A következő vonal-sor a felületosztás , amely a textúra és az anyagjelölés szolgálatában áll - utalva a halmazállapotokra és azok határaira. (A felület-hiányokat is - pl. ablakokat - ez a háló jelölné ki!)
|
|
|
3. Az árnyalástól kezdve alakul át a tisztavonal-rajz tónusrajzzá ; az "alsó" rétegen a kisebb felület-egyenetlenségeket fejezzük ki a helyi árnyékokkal .
|
|
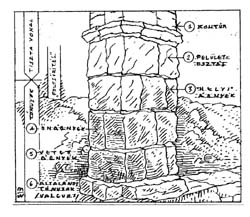
|
4. Az önárnyékok tisztázzák a fényirányokat, a síkok egymáshoz viszonyított helyzetét - a "közbülső" rétegen. A vetett árnyékok segítségével tovább mélyítjük a teret, s még inkább elkülönítjük a térsíkokat egymástól - a Tér differenciálódik. Az árnyékképzés e szakasza is a vonalháló középrétegében helyezkedik el.
|
|
|
5. Végül a "felső" vonalréteg feladata az általános tónus megadása; evvel fejezzük ki pl. az anyagok szín-különbségét.
|
|
|
|
|
| 2.1.4. REDUKCIÓS LÉPÉSEK A RAJZOLÁS GYAKORLATI FOLYAMATÁBAN |
| |
A negyedik oszlop a rajzolás folyamatában keresi a "ferdékhez" vezető utat.
A rajzolás előkészítésből és továbbfejlesztésből áll. Táblázatom címkéi helyenként átfedik egymást.
Hogyan kapcsolható a környezet térhálós redukciója a rajzolás előkészítéséhez?
Meggyőződésem, hogy az előkészítés lépéseivel gondosan kell foglalkoznunk, mert ezek a rajz eredményességére döntő hatást gyakorolnak.
Ide tartozó fejezetek: a " Témaválasztás ", a " Tárgy és Környezetének Együttese ", a " Helyes Leülés " ismertetése. Ekkor tudatosíthatjuk a felezősík fogalmát - utalva táblázatunk VETÍTÉS-oszlopában szereplő képsík-magyarázatára is.
Ezután valóban hozzáfogunk a rajzhoz: egyféle sík-kompozíciós feladatként - a főirányok bevezetésével - felosztjuk a rajzfelületet. A rajz teljes felületét a befoglaló forma és a környezet (előtér, háttér és oldalmezők) összessége adja. (1.2.7.) |
| |
Az alaphálót ebből a negyedik megközelítésből úgy világíthatom meg, hogy az ábrázolandó tárgyat előbb becsomagoljuk, s így a cifra sziluett "bebábozódik". Ez az első vázlat ködös bizonytalansága: a "befoglaló forma" keresésének előjáték-szakasza, amikor a fő arányokat keressük meg. Ezután a képletesen "hálóba göngyölt" tömegeket - a FŐIRÁNYOK segítségével - párhuzamos síkok térirány-rendező deszka-táblái közé csomagoljuk. Íme a kocka-modulra visszavezethető "konténer", amelyből - a részletek kidolgozása során - az eredeti formát kibontandó!
Kivágjuk a " negatív foltokat ", tagoljuk a kontúrt , s megkeressük a belső pontokat. Ez a befoglaló forma jelentősége.
Michalangelo kőtömbből félig kiszabadított rabszolgája nagyon alkalmas példa a "dobozolásra": a kőfejtő réteg-sávjának továbbosztásából való az a nyers hasáb, amelynek határoló síkjaira - a kisebbik oldal alapegységét legnagyobb közös osztóként modulnak véve - rátesszük a négyzethálót.
Vegyük például a HÓESÉST: a fehér paplan varázslepelként uniformizálja a tárgyakat (pl. mindenfajta gépkocsit legömbölyített peremű hasábbá "demokratizál"). A Természet eszköztára végtelenül változatos: néhány pillanatnyi alkonyfény... néhány órányi hóesés... néhány évtizednyi homokréteg s hozzá a távolság levegő-perspektívája: a fény, a távlat és az idő a legnagyobb "csomagolók". |
| |
A táblázatban tovább haladva az "aránymérés" szempontjából vizsgálva folytatom a képmező síkidomokra való bontását. Eszerint jól mérhetők a derékszögű háromszögek és a párhuzamos oldalpárú négyszögek. Az "egyéb" sokszögeket egyszerű geometriai formákra (EGF) tördelem. Módszerem a töréspontokra illesztett főirányok - mint osztó-vonalak - alkalmazása.
Egyszerű geometriai formáktól az aránymérésig közvetlen átmenet mutatható ki. Ebben az oszlopban is tiszta vonalakig redukálom a távlati rajz mozaikokra tördelt összességét.
Miután a fentiek szerint négyféleképpen is eljutottam a tiszta vonalhoz, a táblázat közös alsó sávját a vonalfajták osztályozásának szentelem. A vonalak lehetnek egyenesek vagy görbék . A görbéket átmenetileg húrok és érintők segítségével egyenesekké alakítom.
Eljutok az egyenesek halmazáig. Rajzbéli egyeneseinket két csoportba osztjuk: vagy a főirányok kategóriájába tartozó függőlegesek és vízszintesek - vagy pedig ferdék. A lap széleivel párhuzamos egyenesek rajzolása csak "kéztartás és rutin" kérdése.
Vizsgálódásom központi tárgya a " ferdék " vonalcsoportja lesz.
A fenti táblázattal a ferde vonalak jelentőségét kívántam bizonyítani. Oktatási feladatunk a szerkezeti ferdék fontosságának tudatosítása és dőlés-mérése. Ezt ismerteti a táblázat záró-képe - hagyományos módszerrel illetve az új megközelítés szerint.
A két módszer között az a fő különbség, hogy a kis szakaszokkal dolgozó és bizonytalan elemeket tartalmazó, "ceruzás-méréshez" képest (lásd 1.2.12 -14.) az arányméréses megközelítés pontosabbnak ígérkezik: a szakaszokat kinagyítja, a képsíkot tudatosítja, azaz a kezdeti időszakban egyaránt alkalmasnak látszik oktatói demonstrálásra és hallgatói önellenőrzésre. |
|
| 2.2 FERDE VONALAK DŐLÉS-MÉRÉSE |
| |
| 2.2.1. A KÉPSÍKBELI FERDE VONALAK OKTATÁSÁRÓL - A FERDÉK ELŐFORDULÁSA |
| |
A ferde vonalak képezik vizsgálatom tárgyát. Ferdeségük mértékét a főirányokhoz képest határoljuk be.
A ferdék közül elsősorban az alapvonal-háló perspektivikusan torzult elemeivel, a legnagyobb alá- ill. rálátások, azaz a mértékadó ferdék képében megnyilvánuló összetartások ill. rövidülések jelenségével foglalkozom. Ezek a ferdék felelősek a kétdimenziós rajzlapon kialakuló mélységi hatásért: a harmadik dimenzió csalóka látszatáért.
A többi ferde vonal vizsgálatára csak azután kerítsünk sort, hogy a környezet irányt adó térfalait, illetve a tárgyak alapsík-hálózatának rendszerét - a befoglaló formán keresztül - már tisztáztuk; hiszen minden tényleges ferdét főiránybeli szomszédaihoz képest érzékelünk dőlőnek. |
| |
|
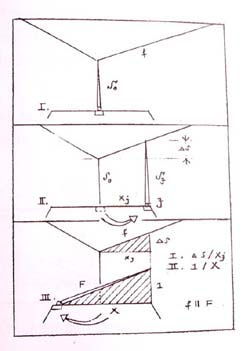
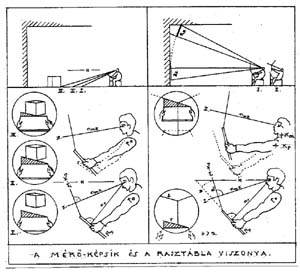
A FERDE-JELENSÉG MAGYARÁZATA
A tárgyképsíkkal (T-Ks) szöget bezáró vízszintes egyenest (OB), - a kocka, mint a térháló alapmoduljának talpnégyzet-oldaláról van szó - azért látjuk ferdének a saját mérő-képsíkunk (M-Ks) széleihez képest, mert síkvetület. A távolabbi sarokra (B) irányított "megfigyelő" nézősugarunk (nmb) a tárgy-képsíkot az alapvonal (AV) felett (B') pontban döfi, melyet mi magasabbnak észlelünk Bav-nál.
Ezért az OB' szakaszra rálátunk. |
|
| |
Aki belekóstolt már az arányméréses módszerrel való ferde-vonalak kikeresésébe, szabad szemmel is egyre-másra fedezi fel a derékszögű hálóhoz viszonyított egyéb kontúrvonalak ferdeségét - képsík rácsán át szemlélve környezetét.
Hol fordulnak elő leggyakrabban a szabadkézi rajzoktatás tanmenetében szerkezeti ferdék ?
A ferdék csoportosítását a rajzolási sorrend miatt részletezem, mert a rajz szerkezeti felépítése szempontjából a fő- és mellékrendszerek között különbséget kell tenni.
TÁRGYTAN:
- Szögletes Testek (a "kockatan" elemei: négyzetlapok, hasábok talp-rálátások, torony-alálátások, stb.)
- Íves testek (az előzőek tér-hálójába írt rendszer szerint: a körök négyzetbe, a hengerek hasábba írhatók -továbbá pl. az ellipszis-tengelyeinek dőlése, stb);
- Bútorrajz (tengelyek, lapok, befoglaló formák, rálátások, stb.);
- Csendélet (a különböző síkok egymáshoz képest változó koordináta-rendszerei, stb.);
TÉRTAN:
- Belső terek (szobasarok-alálátások, ablaksor-rövidülések; lépcsőkarok, lejtők, stb.)
- Külső terek (utcafalak mértékadó párkány-alálátásai, lábazatok meredeksége, tetők stb.) |
| |
| A mértékadó ferdék oktatásának jelentősége |
| |
Okuljunk a típushibák tanulmányozásából! Állandó küzdelmet folytatunk - még a felsőbb évjáratok hallgatóságával is - egyes makacsul visszatérő típushiba -csoportokkal. A természet utáni távlatrajz alap-problémája az adott nézőpontnak és szemsíknak egyedül megfelelő helyes mélységérzet keltése; de, mivel az iránypontok gyakran kívül esnek a rajztáblán, helyzetüket meg kell becsülnünk.
A típushibák nagy része a kétiránypontos perspektíva ferde vonalainak hibás megítélésére vezethető vissza. Ha a rá- illetve alálátás ferdéit rosszul rajzoljuk meg, minden utólagos szépítgetés kárba vész.
Az összetartó vonal-nyaláb egyenesei (a valóság párhuzamosai) a távlati képen mélység-érzetet keltenek, ha jó helyre képzeljük az iránypontot. Ilyenek például épülethomlokzat esetén: a födémperemek, az ablakok párkány- ill. szemöldökvonalai.
A szög-csúcshoz tartozó két szélső értéket kell elsősorban helyesen meghatározni - hová essék a képzeletbeli enyészpont? A többi összetartó egyenes már magától "adódik" - ha a mértékadó rá- ill. alálátás ferdéit rögzítettük.
A feladatok másik nagy csoportja: a vetületekből való távlati kép-helyreállítások, amelyeknek szerkezeti tévedései - mind az alap-térháló rossz kocka-"indításaira" redukálhatók. Hányszor mondjuk: "Nem elég mély a távlati hatás"... "Nem elég meredek a legnagyobb alálátás"... Túl magas ... vagy túl szűk a tér ("De mennyi az a túl ?"). A diáknak pontosan meg kell tudni mondanunk, mennyi a tévedése.
Ezeken az általános típus-hibákon leszűrhető közös eredet. Minden visszavezethető a tárgy-kocka és a térbelső-mint-kocka főirányainak csomópontjáig ; az "Y"-pontban összefutó élek viszonyaihoz (2.1.1.). Meggyőződésem, hogy a képsík-beli FERDÉKET kell egyszer s mindenkorra tisztába tenni! |
|
| 2.2.2. A FERDÉK DŐLÉS-MÉRÉSE - HAGYOMÁNYOS MÓDSZERREL |
| |
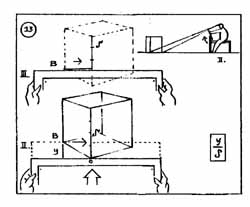
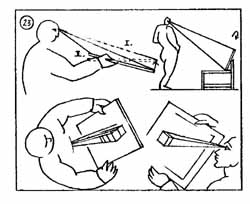
A ferdék megfigyelésére és a látszólagos "dőlés" mértékének tudatosítására régóta használatos az a hagyományos módszer, amely a "nyújtott-karos ceruzás mérés" néven írható körül (ld. 2.3.12-14).
A szabadkézi rajzolás tisztavonal-fázisában számunkra a látvány bizonyos sorrend szerint kiválasztott és egymáshoz viszonyított vonal-szakaszai fontosak.
A klasszikus módszer előnye abban rejlik, hogy a ceruza kéznél van, s a karnyújtás is könnyen elvégezhető. Hátránya viszont az, hogy sok benne a bizonytalansági tényező: a fej és a ceruzával súrolt sík távolsága mobil, a ceruzán a hüvelykujj-körmével behatárolt szakaszméret korlátozott.
|
| |
|
Ezen a linómetszeten - oldalnézetben és a rajztábla felől - mutatom be a "hagyományos" dőlés-mérési módszert: a rajztábla felső peremét alapvonalként használva vízszintesen vetítek (ld. 1.2.12.). Az egyik legjellemzőbb perspektíva-alapjelenség (mely szerint a párhuzamosok összetartanak, s mint ferdék jelennek meg képsíkunkon) szabadkézi "megfogása" ez; táblaemeléses alapvonal-képzéssel. A legnagyobb rálátás ferdéjének, mint átfogónak, befogókra való bontása látszik az illusztráción.
|
|
|
| 2.2.3. AZ ÚJ MEGKÖZELÍTÉS |
| |
A fentiekhez képest a javasolt " arányméréses " módszer képes ideiglenesen rögzíteni a megfigyelendő rövidülés jellegzetes adatait. Ez a rajztáblához kapcsolt virtuális mérő-képsík felületén történik, ahol az arányok számszerűsítéséhez szükséges szakaszméretek összevetése pontosan elvégezhető.
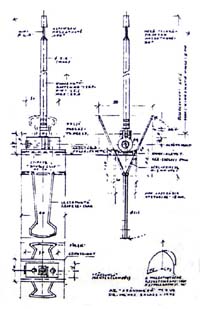
Az eljáráshoz kifejlesztett " aránymérő " az építészeti szabadkézi rajzoktatásban elsősorban a térbeli alapvonal-háló FERDÉINEK mérésére szolgáló oktatási segédeszköz, amely a képsík megjelenítésével áthidalja a "nyújtott-kar" bizonytalanságát (részleteit ld. a. Mellékletben).
Bevezetésével hatékonyan tudatosítható a mérő-képsík és a rajztábla helyes tartása közti összefüggés. Ezek az előkészítő lépések mind a rajz belső rendszerének magját képviselő szemsík biztonságos megállapítását segítik elő, amelyhez a rajzlap széleinek koordináta-rendszere kapcsolódik. |
|
| 2.3. KÍSÉRLETEIM |
| |
Az eddig felsorolt érvek megvilágításában talán már érthető a mottóm: "Mélységet tud, ki ferdét tud". Minden távlati-kép lebontható egy tiszta vonalhálóból szőtt szerkezeti vázig, amely viszont nagyrészt a "ferdék" világába tartozó rövidülés és összetartás alapjelenségek hiteles ábrázolásából építendő fel.
Kísérlet-sorozatom a rajzolási sorrend lépéseinek elemzésére épül. Ha sikerül az oktatás korai stádiumában kifejlesztenem azt a sajátos képességet, amelynek segítségével tudatosul az összehasonlító válogatás és az arányok számszerűsítése; ha sikerül megtanítanom a "ferdék megfogására" a tanítványt, akkor biztos alapokra építhetek a továbbiakban, mert olyan eszközt adok a hallgató kezébe, amellyel biztonságosan tudja megoldani távlattani feladatainak a tiszta vonalhálóból kialakítandó belső szerkezetét.
Így körülhatárolva a cél-területet, egyben felelősségem korlátait is fölvázoltam. Az összes többi távlat-képző módszer, technika és eszköz legyen mások témája!
A szemmérték többé-kevésbé hozott adottság - szorgos gyakorlással azonban látványosan gyarapítható. Tökéletesítése a szabadkézi rajzoktatás egyik fontos feladata. Ennek a folyamatnak az elején kívánok módszertani segédeszközömnek szerepet juttatni. Ekkor a diákok még kíváncsiak és fogékonyak minden újszerű megközelítés iránt.
Kísérleteimben a méréseket - az összehasonlíthatóság miatt - úgy végeztem, hogy ábrázolandó tárgyakat és tereket vízszintes alapon álló, négyzethálós síkokból felépített kockasor-rendszerrel váltottam ki. |
| |
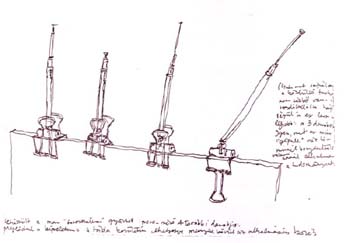
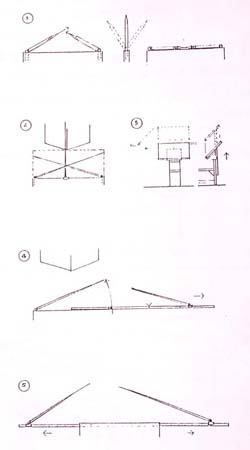
Az új módszertani megközelítésben a Rúdpálcák ötletétől a Háromágú Demonstrációs Eszközön keresztül az Egyágú Aránymérő segítségével jutottam el, mely sorozat végül a Képsík-keret alkalmazásával egészült ki.
Eközben folyamatosan kísérleteztem diákjaimmal az éppen elkészült prototípus-fajtával. A gyakorlatok tanulságait feljegyeztem (ld. Függelékben). A visszajelzéseket az eszköz továbbfejlesztésével rendre felhasználtam. Sokat segített a műszer technikai részének kialakításában orvosi műszerész-munkatársam, Iklódy Albert (SOTE Oktatókórház, Budapest). |
| |
|
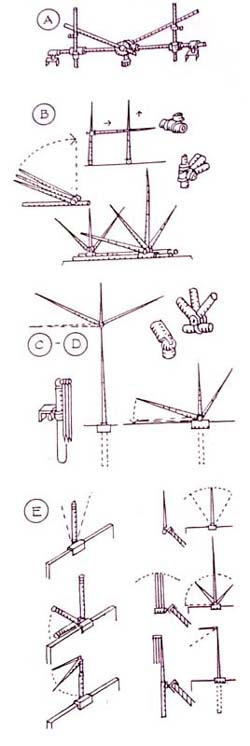
(A) "SZÖGMÉRŐ-KORONGOS RUDAZAT"
Az első vázlaton egy rúdpálcákból összerótt " térlátás-fejlesztő taneszköz " látszik. A vízszintes sík derékszögeinek perspektivikus torzulását szögmérővel ellátott tárcsás rudazattal próbáltam követni. A rajztábla felső peremére erősíthető sínpálcát, azon körbe-forgatható és tetszőleges állásban rögzíthető szög-szárakat képzeltem el. Ez volt az ARÁNYMÉRŐ ötletének csírája.
(B) "MOZGÓ-HÁLÓS KÉPSÍK-RUDAZAT"
A következő vázlat mozgatható irányú és változtatható hosszúságú rudazatot mutat. A teleszkópikus antenna-csápokat az alapvonalon elhelyezkedő tengelyen mozgattam. A rajzoló előtt a látvány fontosabb részeit letakaró képsík-hálót építettem fel ebből az összerakós készletből .
(C) "AZ OSZLOPOS KÉTÁGÚ MÉRŐ"
A tervezés kezdetén egyszerre akartam a térlátás-oktatás négy alaphelyzetét megoldani. Azzal kísérleteztem, hogy a segédeszköz összecsukott állapotban elférjen a zsebemben - használat közben pedig képes legyen mind a közeli, mind a távoli alá-, ill. rálátások ferdéit letakarni. Fő problémát a teremsarok-alálátás jelentette. Ezt egy központi rudazaton , az alaphelyzettel párhuzamosan felcsúsztatott Y-ág alkalmazásával próbáltam megvalósítani. Az eddig felsorolt változatokban részleges képsík-építéssel kísérleteztem.
(D) "OSZLOPOS HÁROM-ÁGÚ MÉRŐ"
Ez a változat négy ágból tevődött össze: a függőleges skála nyakrészéhez terveztem a másik három fiók-ágat felfűző tőcsuklót. Ugyanide került a táblarögzítés is.
(E) "HÁROM ALAP-VARIÁCIÓ"
Így jutottam el az első kritérium-rendszerhez. Műszerészemnek a rajz szerinti kívánságlistát adtam át.
Az alap-típusban egy ág és egy kétirányú csukló szerepel. Másik változata hármas ágat mozgat, ebből lett a "demonstrációs háromágú mérő". Az összetett változat a felsorolt korai ötletek - később zsákutcának bizonyult - változatát mutatja be: a főágon mozgatva a két mellékág közös csuklóját.
Mindezeket a kívánalmakat a körülhatárolt alkalmazási terület (a visszatérő típushibák orvoslásának az igénye) szabta meg. A távlatrajz-oktatásban - az eddig felsoroltakon kívül - sokat vesződünk az egyéb térbeli ferdék (pl. lépcsőkarok, toronysüvegek, konty-tetők, manzárdok, tetőgerincek, vápák, stb.) problémáival is.
|
|
|
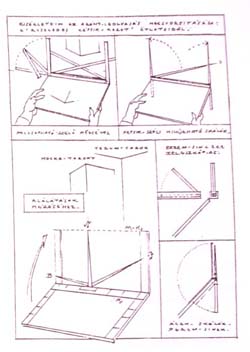
| 2.3.1. ELSŐ KÍSÉRLETEK A HÁROMÁGÚ DEMONSTRÁCIÓS ESZKÖZZEL |
| |
| Ezt az elrendezést az a kiinduló feltétel diktálta, hogy a tőcsukló a vízszintes alapvonalként használandó rajztábla-felsőperem mögé kerüljön, vagyis a három mérő-ág közbezárt szögcsúcsa a perem élen legyen. |
| |
Mindhárom irányú mozgásnak elég szorosnak kell lennie ahhoz, hogy feszesen maradjon ott, ahová a mérés mozzanata állítja: felezősík (Fs), mérő-képsík (M-Ks), ill. mérőágak hosszanti mozgása (M1-2-3 ).
A képsíkban az "f"-re forgatott és a szakasz-hosszra ráállított csáp (F) rövidült volta közvetlen módon is visszaforgatható "S"-hez. Minket elsősorban a ferdének a vízszintessel bezárt szöge helyett a ferdeség mértéke érdekel. E célból a ferdét főirányokba bontott vetületei segítségével jellemezzük. A jobb viszonyíthatóság miatt a két vetületet először nem egymáshoz, hanem az S jelű függőleges skálához (a közeli élhez) hasonlítjuk.
A következő mozdulat: egy szabad csápot virtuális képsíkunkban ráforgatunk a ferde él (f) vízszintes vetületére (x). A függőleges élek között (S és B) mért vízszintes távolságot rögzítettük ebben a fázisban. Ezt a vízszintes irányú összetevőt negyedkörnyi fordulattal hozzámérjük a függőleges skálához: az x/S mérőszám - mint arány - lesz a keresett ferdének egyik meghatározója. A rövidülés miatt ferdének látszó oldalél másik koordinátáját "vízszintes bevetítéssel" állapítjuk meg: azaz szükségünk van az y/S arányára.
Másik lehetőség: a ferde függőleges vetületének bemérésére a harmadik fiók-ágat használjuk (ekkor a többi kar essék takarásban e mögé).
Ellenőrzésképpen a két befogó egymáshoz is hasonlítható (x/y). Ezzel a három aránnyal (x/S, y/S, x/y) egyértelműen jellemeztük a keresett ferdét: most a fenti arányok gondos átvitelével rögzíthetjük rajzunkon a (B) jelű sarkot, s a (BA) szakasz lesz az (f) ferde. |
| |
|
|
| Első kísérleteim módszertani tanulságai |
| |
A ferde-jelenség oktatását kezdő rajzosoknak a következő lépésekben javaslom: |
| |
A) BEVEZETŐ ISMERTETÉS: |
| |
A rajztábla síkjához kapcsolódik a rajzoló mérő-képsíkjának képzeletbeli képernyője, amelyen a szabadkézi perspektívában ábrázolandó látvány legfontosabb elemeit részlegesen beállíthatjuk és mérhetjük. A mérőágakkal a mértékadó (a "legmeredekebb") ferdéket takarásba hozzuk.
A ferde egyenesek átfogókként szerepelnek: a befogók számszerűsített arányát visszük át a rajzra. A szakaszok hosszát első kísérleteimnél az ágakra, illetve a képsík-peremre rögzített csíptetőkkel állítottuk be. A gyakorlat során a hasonló háromszögekkel való aránymérés módszere ennél is hatékonyabbnak bizonyult: a kérdéses ferde szakaszt a képsík-széléig meghosszabbítottuk . |
| |
| B) GYAKORLATUNK TÉMÁJA: |
|
Szögletes váz-testek és padlósíkra helyezett négyzetlapok; a perspektíva alap-jelenségeinek tudatosítása; a mértékadó rálátás meghatározása. |
| |
| C) DEMONSTRÁCIÓ: |
| |
A "háromágú demonstrációs aránymérő" középső csápját a térbeli alapvonal-háló legközelebbi függőleges élére állítjuk (S).
A két szélső ágat a derékszögű csomópont két rövidülő oldalával hozzuk fedésbe. A párhuzamosok összetartás-jelenségét úgy bizonyítjuk, hogy különböző magassági pontokban megismételjük az előbbi, látszólagos szög-torzulás lefedését.
Mivel az ágakat rendre át kell állítani (a vízszintest csak saját szemsíkunknál érjük el), kézzelfoghatóan érzékelhetővé válik a távoli iránypont helye.
Ezután egy olyan közeli padló-négyzetlapot kezdünk elemezni, amelynél az oldalélek látszólagos dőlése jól bemutatható. Az egyik "ferdét" - az alaprajzon jelöljük be, amelyikről szó lesz - bontsuk szét főirányaira, egyenként rátakarva az eszköz ágaival. |
| |
| D) JAVASOLT SORREND: |
| |
Sv - az első ágat függőleges helyzetben ráállítjuk a talppontra (O);
F - a második ággal kis időre lefedjük a kérdéses ferdét, hogy tudatosítsuk a hallgatóban a mérendő egyenes helyzetét - amíg ferdeségének ténye a mérő-képsíkhoz (ill. a csatlakozó rajztábla peremeihez) képest egyértelművé válik;
Xf - a harmadik ág a rövidülő egyenes vízszintes vetületére mutat;
Xf/S - a vízszintes vetület hosszát negyed-körívvel a kezdőskálához mérjük.
Fontos lépés az aránypár hangsúlyozása.
Végül az yf (függőleges vetület) mértékét mutatjuk be. |
|
|
|
| 2.3.2. EGY KÍSÉRLETI RAJZ-ÓRA LEVEZETÉSE (Kiegészítő képzés, I. évfolyam - 1996. nov. 26.) |
| |
A táblai magyarázatot a rövidülés-összetartás jelenségének egy oldalnézetén keresztül való bemutatásával kezdem. (Miért látszanak a távolabb levő távíró-oszlopok - képsíkunkon megjelenve - abszolút méretükben kisebbnek, mint a közeliek?) Ez a rajz különböző képsíkok felvételére is lehetőséget ad.
Utána a tárgy-, illetve térrajzolás oktatásának kulcs-szereplőjét, a kockát elemzem: különböző példákkal illusztrálva, miért vezetünk vissza minden térben ábrázolandót erre a testre.
Mivel a mélységet kifejező harmadik főirány távlatrajzunkon a rajzlap széleihez képest ferde vonalként jelenik meg, ezért ezeknek a helyes dőlésszögben való megrajzolása az a kritikus fázis, amelynek objektív ellenőrzéséhez a kísérleti segédeszközt felhasználjuk.
Az eszköznek már a legkorábbi, háromágú mintapéldánya is alkalmasnak bizonyul a jellegzetes ferde vonalak tárgyilagos kontrolljára. A diák helyére ülök, s az ő nézőpontjából vizsgálom az alapvonal-háló perspektivikus torzulását; így "belerajzolás nélkül" be tudom állítani a vizsgálandó ferde egyeneseket - a rajztábla felső peremére rögzített "aránymérővel". Az arány számszerűsítését a mérő-képsík széléig meghosszabbított mérőág, mint átfogó segítségével mutatom be.
Az első demonstráció során nyilvánvalóvá vált, hogy a derékszögű háromszög befogóinak aránya legkönnyebben a "legnagyobb" befogók helyén, vagyis a képsík szélére illeszkedő háromszögben olvasható le.
A viszonyszám megnevezéséhez a kisebbik befogót kinevezzük egységnek. Gyakorlatban az egységnyi befogót a kézben tartott ceruza-méret képviselheti - ahol a kisebbik befogó éppen ceruza-méretű, odáig tart a hasonló háromszög másik befogója. Az egységnyi befogót ráforgatva, megkapjuk a ferdeség mértékét.
A táblai magyarázat fontos része az alap-kocka főirányainak folyamatos vonallal történő, kétféle nézőpontból történő ábrázolása. Az egyik a tárgy-rajzoláshoz , a másik a tér-rajzoláshoz tartozik.
A ferde vonalak tudatosításához az alaphálóra szerkesztett beállítás felülnézeti megrajzolása is szükséges. Külön nyíllal bejelölöm a megfigyelés irányát, a rajzoló figuráját. A nézési irányra merőlegesen berajzolom a figura mérő-képsíkját is, amelyen a térháló torzulásai jelennek meg. Az alapvonal-rendszer közeli sarkára újabb képsíkot állítok (felülről ez is a vezérsugárra merőleges, a rajztábla-képsíkkal párhuzamos vonalnak látszik). Legyen ebben a sarokban is kocka-egység - így annak közeli függőleges éle közvetlenül bennfoglaltatik a tárgy-képsíkban!
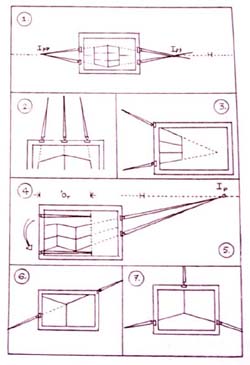
A kísérő magyarázatot két, egyidejűleg fejlesztett táblai rajzzal folytatom. Az egyik kép követi, amit a rajzoló rajztáblája felső peremének környékén lát: az "aránymérő" ferdéje ráilleszkedik a látvány rövidülő alapháló-egyenesére. A betűjelek megegyeznek a szomszéd ábrának jelöléseivel, ahol a folyamat távlati képe készül. Ezt látja a rajzoló... és ezért látja így a rajzoló! |
| |
|
A betűk jelentése:
0 - a térbeli három főirány közös talppontja - a közeli függőlegese alsó pontja;
S - a közeli függőleges él mértékadó skálája;
J - a jobboldali "ferde" szakasz végpontja;
J'- a rajzoló J-re irányított megfigyelő-nézősugarának döféspontja a tárgy-képsíkon;
y - az OJ'-szakasz függőleges vetülete;
x - az OJ' vízszintes vetülete;
Y és X - az előbbiek mérőképsík-beli, kinagyított megfelelői. |
|
|
Érdemes a rajztábla-nézet alá a kinagyított, hasonló derékszögű háromszöget is odarajzolni, hogy a vonalkázott kis-háromszög és a képsík széléig meghosszabbított átfogóval előállított nagyháromszög hasonlósága belevésődjön a diákok tudatába.
A távlati kép ábrája érzékelteti, miért kell "irányba ülni"! A nézősugarak perspektivikus képéhez azok padló-vetületeire is szükségünk van: így demonstrálhatjuk az "emelkedőnek" látszó jobboldali padlószakasz ferde megjelenését (vagyis a J' döféspont keletkezését) a tárgy-képsíkon. |
| |
A magyarázó ábra készítésének a sorrendje: először a figura rajztábla-fölötti "V"-jét rajzolom meg; azután a megfigyelő néző-sugarak következtek. Ahol a rajzoló szeméből indított és a tábla peremére illesztett nézősugár beledöf a padlóba, felépítem a tárgy képsíkját, párhuzamosan a rajztábla-képsíkjával. (Itt már ügyelnem kell a kis és a nagy képsík-ernyőket képviselő téglalapok hossz-oldalainak összetartására is!) A 0 - pontra rajzolom a nagy képsík "V"-jét (azaz az eredeti méretű közeli függőleges élet (S) és a talpából kiinduló jobboldali ferdét (OJ').
A tárgy-képsíkon a J' döféspontjából függőlegesen visszaereszkedhetek a padlóra (P), s onnan a J-re irányított néző-sugár padlóvetületével visszakerülök a rajzoló talp-pontjáig (T). A PT szakaszt a nagy képsíkon túl meghosszabbítva tűzhetjük ki a padlón a valóságos jobbfelöli kocka-sarkot (J), mely a perspektivikus nézősugár (n) és annak az előbbiek szerint megszerkesztett padló-vetületének (n') metszéspontjában lesz.
Ezzel a valós kocka-alapéllel (OJ) dolgozva, most már megrajzolható a teljes alsó négyzetlap - s a harmadik nézősugár (ns) által a nagy képsíkon korábban kitűzött közeli kockaél (S) segítségével kiemelhető a padlósíkból az egész kocka, mint az eredeti beállítás tárgya.
Eközben mindkét ábrát azonosító betűjelzésekkel egészítem ki. Párhuzamos fejlesztésük időt enged arra, hogy a hallgatók eljussanak az ellenőrizhetőség készültségi fokáig. A kívánt eredményt szem előtt tartva, a képtől a tárgyig visszafelé szerkesztettem. A leírt sorrendet célszerű betartani ahhoz, hogy az összetett magyarázó ábra, - kényes pontjainak takarás-mentes megjelenítésével - sikerülhessen.
A természet utáni rajzolás menete általában folyamatos és összetett művelet: ideje egyrészt a téma megfigyelése (felemelt tekintet), másrészt a rajzra irányított tevékenység (lehajtott fej) között oszlik meg. Az oktatás szempontjából lényeges a ráfordított össz-idő maradéka. is: ez pedig a tanár magyarázatának hallgatása. Ne legyenek túlzott illúzióink: a leglelkesebb magyarázat sem tudja, egy bizonyos küszöb-értéken túl, lekötni a "rajzolni vágyó" diákokat.
Ezért az óra-kísérő magyarázat nagyobbik részét kitevő táblai rajzoláshoz olyan szöveges kiegészítésnek kell párosulnia, amelyet még akkor is képes követni a hallgató, ha nem látja folyamatosan a rajzoló tanár mozdulatait, mert közben rajzol. A táblai rajz kísérő szövege akkor hatékony, ha a jeles pontokra egyértelmű megnevezéssel hivatkozni tudunk.
Ezután a háromágú ARÁNYMÉRŐ kísérleti használata következett: A bevezető demonstráción túl elegendőnek bizonyult egyetlen mérőág alkalmazása, hiszen általában a "legnagyobb" rá- ill. alálátás ferdéit kívánjuk pontosan bemérni. Ha túl lapos a mérendő ferde, akkor inkább "átlót" mérjünk, melyet azonosítsunk be a vetületi alaprajzon is.
A mérés befejező fázisa: az ellenőrzött ferdét visszamásoljuk a rajzlapra. Az O-pontra vízszintes fektetünk, s ezt meghosszabbítjuk a lap széléig. Az így előkészített két befogóra ráépítjük az átfogót: a mért ferdét. Most látszik igazán, mennyi az eltérés a rajzolt feltételezés és a tényleges alapháló-torzultság között? A különbséget érdemes színezéssel kihangsúlyozni. |
|
| 2.3.3. AZ ELTÉRÉSEK SZÁMSZERŰSÍTÉSE |
|
Egy másik kísérlet alkalmával a legnagyobb rálátást mérjük a padlónégyzet-hálón, két iránypontos perspektívában. A centrális perspektívát rajzolók (akiknél a kijelölt szakasz rövidülés-aránya 1/10-nél kisebb lett volna), a mértékadó átlót figyelik meg.
A gyakorlat lényege az, hogy az alapvonalháló egy bizonyos, erősen rövidülő részére koncentrálunk. A perspektivikus torzulás mérendő helyét az összes táblai vetületi rajzon előre bejelölöm.
A kísérlet során bebizonyosodik, hogy a diákok a dőlés-mérés hitelesítéséhez a segédeszközt elfogadják. Mivel az ellenőrzés az ő szemszögükből nézve történik, esetleges tévedésükről helyben meggyőzhetőek.
A rajzolási sorrend tudatosítását egy általános demonstráció során végeztem el. Felhívtam a figyelmet arra, hogy a szemmértékkel való rajzolás kifejlesztésének ez a módszer csupán közbülső állomása, amely a szakaszokra bontott "aránymérés" beidegződését kívánja elősegíteni.
A különböző képességű és elő-képzettségű diákoknál természetesen eltérő eredményekre számíthatunk. Az oktató feladata annak megítélése, hogy a térbeli alapvonal-háló perspektivikus ábrázolásának elsajátításában mikor és hányszor szükséges a fenti demonstrációs módszer alkalmazása.
A kísérlet során a mérő nélkül rajzolt (R), illetve az eszközzel mért (M) rövidülés különbségét a lap széléig meghosszabbított átfogókkal és a bevonalkázott, illetve kiszínezett mezőkkel látványosan tudtam demonstrálni.
Az eltérések túlnyomó többsége a rajzolt meredekség alábecsüléséből adódik: meggyőződésem, hogy rajzoktatásunknak a távlati alap-jelenségek fokozott mértékű tudatosításában van újszerű módszertani megközelítésekre szüksége.
Az alábbi képlettel számszerűsíthetők az eltérések (E): |
| |
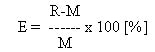 |
| |
ahol R = a "rajzolt" függőleges befogó (Y) - amit a diák eszköz nélkül rajzolt;
M = a "mért" (Y) - amit a diák helyéről az oktató mért és visszarajzolt, a diák pedig - újra leülve - "ellenjegyzett". |
|
A jobb áttekinthetőség kedvéért a derékszögű háromszögek képsík-aljához illeszkedő közös vízszintes befogóját (X) egységnyinek vesszük, ekkor az ehhez kapcsolódó mért, illetve rajzolt befogók dőlés-szöge közti különbség jól színezhetővé válik.
A peremen fölvett felezési pontokkal (illetve, szükség esetén további felezésekkel előállított negyed, nyolcad stb. pontokkal) az eltérés "számszerűsíthető". (Legyen a meredekség jól kimondható törtszám!)
A mérés célja az, hogy a diák elismerje, és egyúttal helyesbítse a rövidülések-összetartások észlelésében elkövetett tévedéseit. A mérés lépéseinek egyénenkénti megismétlése a módszer lényegéhez tartozik: mindenki csak a saját nézőpontjának, saját szemsíkjának és a saját rajzának hisz. A diák értékeli a részletes, személyének szóló ("testre szabott") foglalkozást és azt az újszerű demonstrációs eljárást, amely rajzának érintése nélkül nyújt tárgyilagos, konkrét törtszámokkal alátámasztott bírálatot.
Ennek következtében - kísérleteim szerint - a tanítvány az alap-jelenségek ábrázolásában eredményesebbé válik, s helyesebben rögzíti a térbeli alapvonal-hálót ill. annak eltéréseit. Bizonyos "küszöbszint" elérésével már eszköz nélkül is tudja már, mit kell megfigyelnie.
A gyakorlatban nem szükséges a rajzolt és a mért befogókat centiméterben mérni és számológéppel (a fenti képlet alapján) az eltérést kiszámolni - hiszen műfajunk: szabadkézi rajz! Számunkra elegendő pontosságot nyújt a törtszámokkal való arány-megállapítás is. Az aránypár-elvű visszarajzolás miatt mégsem mondhatunk le bizonyos számolgatásról: szabadkezes elrajzolások a laikusnak is azonnal szemet szúrnak. |
|
Mintalap az arányméréses kísérlethez.
BME. Rajzi Tanszék, 1996/97. tanév. |
|
|
|
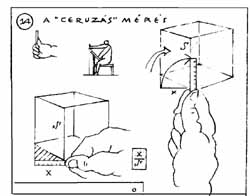
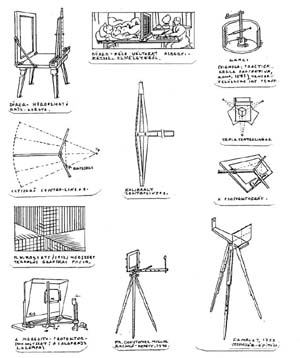
| 2.3.4. AZ EGYÁGÚ ARÁNYMÉRŐ BEVEZETÉSE |
| |
A "háromágú demonstrációs mérőeszköz" használata során szerzett tapasztalatok alapján megszületett az egyetlen mérőággal felszerelt oktatási segédeszköz első példánya (1997. január 17-én). A bíráló tekintsen el a prototípus házilagos jellegétől: sokkal kisebbnek és kecsesebbnek képzelem el a sorozatgyártás darabjait. A mérőág lába olyan, peremcsipesszel egybeépített, gömbcsuklón fordulna, amelynek igényes kialakítása formatervezőre vár. |
| |
Az első mérést a műszerész műhelyében végeztem. A nagy belmagasságú, hasáb alakú tér felső térsarkait vizsgáltam. A toronyszerűen felhalmozott tárgyak felső éleinek, illetve a térbelsők alálátásának az esetét próbáltam ki.
A mértékadó (ferdének látszó) élre, előbecsléssel, "ferde-közeli párhuzamost" állítok a rajztábla alaphelyzetéből. Ellenőrzés-képen (alapvonal-emeléssel) "után-igazítom" az előbecsült mérőágat, majd a rajztáblát visszaengedem az eredeti rajzolási helyzetbe. A befogókon leolvasom a dőlés arányszámát.
Ezt az arányt használom fel a rajzbeli ferde rekonstruálásához. Szükség van a térben és a rajzon beazonosított, főiránybeli skálára is (most pl. az ablak vagy más háttér-részlet). Ennek meghatározásához függőleges vetítő-élként is használható a segédeszköz, melyet a rajztábla felső peremén, átállítással , csúsztatok a keresett látványrészlet takarásáig. |
|
|
TÉRBELSŐ ELSŐ SARKÁNAK BEMÉRÉSE, HAT LÉPÉSBEN - EGYMÁST MEGERŐSÍTŐ KETTŐS MÉRÉSSEL
1. A mono-ág ráillesztése a függőleges élre (So );
2. Új talppont keresése az alapvonalon: pl. nyílás a falon (J); vagy a képsík széle;
3. x j bemérése S 0 -hoz;
4. A két függőleges közti különbség: SJ -So megállapítása (DS viszonyítandó XJ-hez);
5. Harmadik talppont-helyről "ferde-közeli párhuzamos előbecslése" (f II F);
6. A jelölt háromszögek hasonlóságának ellenőrzése. |
|
|
| 2.3.5. TÖBB EGYÁGÚ ARÁNYMÉRŐ EGYIDEJŰ HASZNÁLATÁRÓL |
| |
Egynél több egyágú aránymérő birtokában az eddig főleg a ferdék dőlés-helyzetét meghatározó segédeszköz alkalmazási köre kiszélesedik. Gyakorlatilag mind a négy "Y"-típusú alaphelyzet ferdéinek bemérésére alkalmas - mozdulatlan táblatartás esetén is.
Kísérletezzünk pl. 3 db mono-ággal! Vizsgáljuk meg rendre az Y-csomópont egyik ágát!
1. A kocka-alsóarok rálátását az élek meghosszabbításával könnyen be tudjuk fogni (f = F).
2. A torony- alálátás esetében hosszú, "ferdeközeli-párhuzamos" átfogót képezhetünk a tábla szélső sarkától indított mérőággal - miközben egy második szóló-ágat a függőleges éllel hozunk takarásba. A harmadik állhat a tábla másik szélén. (Befogó-arányt így kétszer is mérhetünk: Y/X vagy So -Sb /Xb ).
3. Teremsarok- alálátásnál, az előzőekhez hasonlóan, szintén kétszeres biztonsággal mérhetjük a ferdét; A két helyen mért magasságok különbsége: Sb -So . A vonalkázott háromszögek hasonlóak: X viszonyítandó Xb - hez.
4. Teremsarok alsó csomópontja: (hasonló az első esethez) - A rajztábla felső sarkairól indított mono-ágakkal egyszerű a ferde-közeli párhuzamosokat beállítani, majd kölcsönösen befogó-arányokat mérni (a kisebbet egységként lehajtva a vízszintes helyzetű, nagyobb befogóra).
Az oldal-peremeket is talpvonalként használva további alkalmazási területeket nyerünk: pl. az iránypontok és a horizont megkeresése is lehetővé válik. Két szélső ferdét meghosszabbítva éreztethetővé válik az enyészpont. Túl lapos ferdék helyett a meredekebbnek látszó átlókkal foglalkozzunk: az átlók iránypontja hasznos szerkezeti elem.
Párosával használva az egyágú aránymérőt, kezelése egyszerűbbnek bizonyult, mint a háromágúé (ferdék párhuzamosai, Ip -keresés, képkivágás, átlók, térbelső-alálátások, ereszek, tetőgerincek, stb.) |
|
|
|
| EGYÉB ALKALMAZÁSI TERÜLETEK - EGYNÉL TÖBB MONO-ÁGGAL |
| |
A rajzsík-beli vonal-meghosszabbítások esetei:
1. "Mértékadó" ferde egyenesek külső meghosszabbításával iránypontokat (Ipb , Ipj ) és szemsíkot kereshetünk.
2. Szélső függőlegesek rajz-síkon túli meghosszabbításával felkutathatjuk a harmadik iránypontot is.
3. Két szélső ferde kifelé történő meghosszabbításával a térfalat kiterjeszthetjük a rajzon túl. A megnövelt vonalhosszak által keretezett részlet térhatása megnő: könnyebb a rész- tagolásokat (pl. emeletközi párkányokat) besűríteni a kihangsúlyozott szögszárak közé.
4. Jelentős oldaltávolságok rajztáblát keresztező mérésére is alkalmas az eszköz.
5. Ugyanaz, mint az 1. pont - amikor a szemsík (H) kívül esik a rajzsíkon.
6. A rajzon átmenő ferde kétoldali meghosszabbításával a meredekség "kinagyítható".
7. A főirányok meghosszabbításával a tér-sarok tágítható. |
|
|
|
| 2.3.6. A KÉPSÍK-KERETES ARÁNYMÉRÉS MÓDSZERE |
|
Az aránymérővel folytatott első próbák rámutattak a befogó méretek leolvasásának problémájára. Az összehasonlításokhoz valamilyen skálára van szükség. A rajztábla-széli ceruza-bejelölések, ideiglenes papírcsíkok főirány-menti tologatása és egyéb próbálkozások után született meg a kemény kartonból házilagosan elkészíthető KÉPSÍK-KERET. (Utólag nyilvánvaló a rokonság a Dürer- féle, vetítősugár fogalmát magyarázó fametszettel.)
Kisebb formájában korábban is alkalmaztunk hasonló keretet a "képkivágás", a kompozíció, a legmegfelelőbb nézőpont választása céljából.
A nézőke-módszer a mérő-képsíkot kézzel-foghatóan meghatározza - mégpedig azon az alkalmas helyen, amely már elég távol esik a szemtől, hogy a felesleges látvány-sávokat kitakarja - de még elég közel a rajzolóhoz, aki ellenőrző méréseit ezen rendre elvégezheti. Ebben a változatban minden "ferdét" utolérek a képsík kereten belül. A méréseknél mindkét átfogó-végpont szilárdan rögzíthető a keret mentén.
A képsík-keret a leggyengébb rajzolók számára jelenthet segítséget, akiknek a beállított látvány nem "képszerű" - amíg át nem néznek a teljes látómezőt részlegesen korlátozó kereten! Célom a rajz szerkezetének hatékony tudatosítása.
A kerettel kombinált eszköz segítségével "felfedezi" a képsík-beli ferdéket. A függőlegeseket és a vízszinteseket eddig is jól látta, de az ezektől eltérő egyenesekre most tudjuk a " Mihez képest ?" kérdéssel ráébreszteni az abszolút kezdőket, akik - mivel szinte a "kész rajzot" látják maguk előtt, felbátorodva - szárnyakat kapnak.
A fenti eljárással szemléletesen demonstrálható a perspektíva-elmélet. Megidézhetjük Dürer szellemét (kitérve arra is, miért rajzoltatunk egyelőre "kockát" - a reneszánsz aktja helyett?). E lépések biztonságosan elvezetnek a "kockológiától" a bonyolultabb tárgyak és terek távlati ábrázolásáig. |
|
|
|
A gyakorlat mutatta meg a keret méretét. A táblaperem fölé illesztettem a néző-keret alsó sávját. A látótér szélessége ill. magassága kiegészülő takarásokkal módosítható.
A minta-példány a kapható rajzmappa-modulhoz igazodik. A keret belsejébe éppen belefér az A/3-as rajztábla. Jól beváltak a lapszéltől-lapszélig érő (a dupla keret-fal közébe beszorított) közönséges pálcikák is.
A keret kitámasztását - a mellékelt szabásminta szerint - egy maradék karton-csíkkal oldottam meg. A keret síkja úgy állítandó be, hogy hosszanti pereme a téma függőlegeseivel közel párhuzamos legyen.
Alkalmazásának az a fő előnye, hogy a "kész-rajz" - élményét nyújtva, az eredményt megelőlegezi. Rögzíthető a horizont is, mert egyidejűleg többféle és többirányú pálcika-beállítás lehetséges.
Az eddig felsorolt segédeszközök közül - a felső keretsávnak köszönhetően - ez a változat elégíti ki leginkább azt a kívánalmat, hogy a tárgyak ill. terek alálátását (táblaperem-mozgatás nélkül is) mérni tudjuk.
A bemutatott ferde-elemzések közül ez a legirányítottabb módszer.
"Berkesi Tamás rajzol" (KIEG. KÉPZÉS. I. évf.)
A nézőkeret kipróbálása a legnagyobb rálátás ferdéjének méréséhez BME, Rajzi Tanszék. 1996. dec. 12-én |
|
|
|
| 2.3.7. A HÁROMFÉLE SEGÉDESZKÖZ ÖSSZEHASONLÍTÁSA |
| |
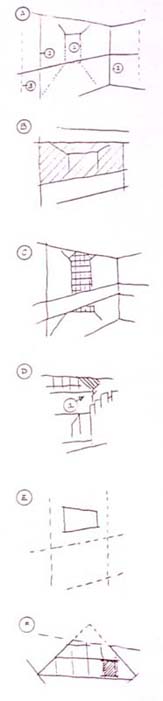
A bemutatott kísérleti eszközöket az alábbi táblázatban vetem össze egymással - alkalmazhatóságukat a négy " alapeset " vizsgálatára szűkítve elemzem. |
|
|
|
A táblázat függőleges oszlopaiban az eddig tárgyalt oktatási segédeszközök a rajzoló felől nézett rajztábla-felsőperemmel szerepelnek. Mivel mindegyik ferde-vizsgáló alapeset helyzet-stabilizáló vízszintesünkre épül, a mezők közti összekötő elem a látvány és a rajz közös határvonala.
Az áttekintés vízszintes soraiban a tárgy- ill. térábrázolás redukált sémái láthatóak. Az alá- ill. rálátások "ferdéit" egy-egy pozitív ill. negatív saroknál tanulmányozom. |
| |
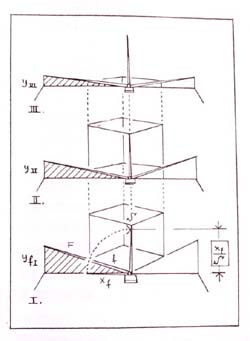
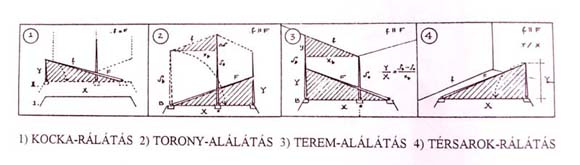
A redukált térbeli vonalháló négy alaphelyzete a következő:
1. A kocka közeli, alsó sarka (a legnagyobb rálátás);
2. A kocka-torony legfelső sarka (a legmeredekebb alálátás);
3. A terem-belső felső sarka (távoli alálátás);
4. A terem-belső alsó sarka (távoli rálátás). |
| |
Az első oszlopban a vizsgálandó alaphelyzeteket egy-egy "Y"-nal (ill. fejreállított változatával) jelölöm. A függőleges él (az "Y" lába) függőlegesnek látszik. Az "Y" karjainak a vízszinteshez viszonyított helyzetéről van szó.
A táblázat második oszlopában a sematikus metszetek a szemmagasság és a kocka-sorok viszonyát mutatják be. Az alap-helyzeteket egymásból származtatom. Ahogy az oktatás folyamán az egyszerűtől az összetett feladatok felé haladunk, úgy építem fel a tárgy-modulból a "teret": (A környező tér belmagasságáig a tornyon át jutok el.) A léptékadó figura méret-váltása érzékelteti a tárgykocka "felnagyítását" - akkorára, hogy elférjen benne a terem!
A szemlélő közel átlós irányból (félprofilból) nézi a tárgyat ill. és a tér-belsőt úgy, hogy egyik lap sem párhuzamos képsíkjával. Az esetek összevethetősége miatt az "Y"-csomópont felfelé vagy lefelé mutató ágai közül rendre a baloldali kart vizsgálom.
A hagyományos oktatási módszer szerint az elemzést a " rálátással " kezdem. (A padlósíkon álló nagykocka alsó négyzetlapja - távolabb lévén a rajzoló szemsíkjától - jobban ferdülő egyeneseket produkál, mint a fedlapja. Meredekebb ferdét könnyebb mérni, mint a főiránytól alig eltérőt! |
| |
Az ábrákhoz írt betűk értelmezése:
S - a függőleges skála (leginkább rész-beosztással használható);
f - a mérendő (ferdének látszó él);
F - a ferdét lefedő, a mérő-képsík széléig meghosszabbított mérőág;
x - a mérendő ferde vízszintes összetevője;
y - a mérendő ferde függőleges összetevője;
X - az eszköz mérőágának (mint átfogónak) vízszintes összetevője;
Y - a mérőág karjának a függőleges összetevője; továbbá
f = F a mérendő ferde közvetlenül takarható a mérőággal;
f || F előbecsléssel "ferdeközeli" párhuzamos, perem-emeléssel véglegesítve. |
| |
Az új módszertani megközelítés szerint mindhárom demonstrációs ill. önellenőrző segédeszköz közös alapelve az, hogy a térbeli alapvonal-háló ferdének látszó egyeneseinek dőlés-elemzése során, a felnagyított befogókat (az átfogó meghosszabbításával) kivetítem a mérő-képsík peremére; azaz a ferdültség mértékét a "ferde"-vonal főiránybeli vetületeinek összevetésével számszerűsítem.
A használhatóság köre jelentősen bővül, amikor felszabadítjuk a rajztábla kezdeti mozgatásának tiltását. Gyakorlottabb korunkban a rajzosok ezt meg is teszik a perem-emelés közben is; biztonsággal megtartva az eredeti, szemsíkkal párhuzamos alapvonalukat. |
|
| (A) A "HÁROMÁGÚ DEMONSTRÁCIÓS ESZKÖZ": |
| |
Bár a kezelése bonyolultabb, mint a mono-változaté (mindkét kezünkre szükség van a beállításhoz), a másik két eszköztől eltérően a "ráforgatás" és a "kétoldali összehasonlítás" mozdulata is benne rejlik, hiszen képes a megfigyelés pillanatait " egymásra-vetíteni ". Ágaival mindhárom térbeli főirány egyszerre bemutatható.
A 1 - Egyszerre befogható mindkét oldali ferde (alkalmas a "demonstrációra", hiszen látványosan követi a szögek változását). Kétféle mérési lehetőség adódik:
|
I. - fix táblaperemes előbecslés; (f II F)
II. - emelt táblaperemes közvetlen ráállítás; (f = F) |
| |
A 2 - A magasság külön is mérhető, a 0-pontra ráállított mérőággal. Gondosan kell a "felezősík-pozíciót" tartani, mert nincs mihez fogni a felső ágvéget. Másik lehetőség: magasság-különbséget mérünk a talppontnál (So ), attól xb távolságot lemérve a második ággal, újabb magasságot fogunk be (Sb ). |
| |
A 3 - Ha a mérendő ferde (f) és a mérő-ág (F) közti távolság túl nagy és a párhuzamosság bizonytalan - az elő-becslést kövesse az ún. "megemelt peremvonalas utókorrigálás". Érdemes két helyen magasságot mérni, majd különbségüket összehasonlítani a vízszintes mérőhely-távolsággal. |
| |
I - Talppont-áthelyezéssel; a magasság-különbséget (So - Sb) viszonyítjuk x-hez;
II - A talppont So-nál marad, majd fix peremtartással a 2 ágat széttárjuk, azaz kettős ferde-előbecslést alkalmazunk. (A szem kövesse a falsíkon túl meghosz-szabbított sarokélet, mintha tükörfalról lenne szó!) |
| |
A 4 - Fix peremtartással: az első mérő-ágat függőleges S-re állítjuk, a talppont (0) alá; majd a bal és a jobb mérőágat párhuzamosra állítjuk a képzeletben a sarkon túl meghosszabbított padló-élekkel. Így egyidejű, kétoldali mérés lehetséges: 1/xb , illetve 1/xj . |
|
(B) AZ "EGYÁGÚ ARÁNYMÉRŐ" |
| |
Gyakorlati ferde-mérésre fejlesztettem ki, közvetlen "ferde-lefedéssel" vagy közvetett, "ferde-közeli párhuzamos" beállítással egyszerűen használható. |
| |
B 1 - Háromféle beállítás lehetséges:
I - Fix táblaperemes, előbecslés, ekkor f II F
II - Emelt táblával, fedésig: f = F
III - Emelt táblával, talppontig: f = F
(Az ellenőrzéshez elegendő a II. állásig megemelni a táblaperemet.) |
|
(C) AZ ARÁNYMÉRŐVEL KOMBINÁLT KÉPSÍK-KERET |
| |
Magasság-különbségek mérésére, vízszintes bevetítésekre, szemsík-keresésre, mindenfajta egyenes képsíkbeli "rögzítésére" alkalmas eszköz. A képsíkok párhuzamosságának beállításában is segít. Kerületmenti skálái igen pontosak. Képkivágást (pl. előteret) megkeresni tanít, továbbá a mozdulatlan rajztábla-tartásra nevel.
3 - Az alálátás ferdéjét átfogónak véve, egy vízszintes pálcika kerethez való illesztésével, tábla-mozgatás nélkül képezhetünk "alapvonal-befogót" (X).
Ha a képsík-kerethez közelebb hajolunk, kitágíthatjuk látómezőnket. Így segíthetünk befogni pl. a "túl-magas" tornyot. Fontos az x-hely bemérése, hogy a mért arány rajzlapra való visszamásolásánál legyen mire építkeznünk!
C 4 - Terem-sarok-rálátásnál egyaránt gyümölcsöző a "ferde-közeli párhuzamos", vagy a közvetlen ráállítás is. Az oldal-skálán kétfelől mért magasságok különbsége adja a vonatkozó Y-értéket. Egy vízszintessel közvetlenül is lezárható a nagyháromszög talpa (- mintha virtuálisan megemeltük volna a képsík-keret alját!). |
|
| 2.3.8. A "MÉRŐ-KÉPSÍK" ÉS A RAJZTÁBLA-SÍK KÖZTI SZÖGKÜLÖNBSÉG BEÁLLÍTÁSÁRÓL |
| |
Az arányméréses módszerhez a mérő-képsík helyzetét a "megfigyelő" nézősugárra (nm ) merőlegesen, negyed-körívnyi (0° -90° ) tartományban kell felvenni. Ha ezt elmulasztjuk, a dőlés-mérés eredménye hamis lesz. |
| |
Vizsgáljuk meg egyenként, ebből a szemszögből, a négy alaphelyzetet: |
| |
1. eset (kocka-talp, közeli rálátás) Ha a mért él közel van az alapvonalhoz, a mérőág talppontja közvetlenül a rajztábla peremére kerül - a vizsgált ferde meghosszabbításában.
Ha a vizsgált sarok feljebb van, "ferde-közeli párhuzamost" állítunk. (Ezt az elő-becslést perem-emeléssel ellenőrizzük.)
Talp-élek perem-közeli vizsgálatánál is számít a mérő-képsík (M-Ks) és a rajztábla-sík (Rs) közti szögkülönbség. A helyes képsík-beállítást ezekben az egyszerű helyzetekben kell begyakoroltatnunk. |
| |
| 2. eset (kocka-torony, közeli alálátás): Az előzőek miatt különösen fontos a megfelelő tárgy-távolság kiválasztá- sa. (Ne üljünk túl közel az alálátások talpához!) |
| |
3. eset (terem-belső felső sarka, távoli alálátás): A mellékelt oldalnézeten követhető, hogy a teremsarok éleinek (f) ellenőrző mérésekor (F) nem torzul az átfogó dőlésszöge, ha merev törzstartásban - alapvonal-képzés céljából - megemeljük a tábla-peremet. A mérőág talppontját a szélső peremsarokra állítva csökkenthető az után-igazításhoz szükséges perem-emelés mértéke (II).
Ennek az a feltétele, hogy a mérő-képsíkunk az előbecslés kiinduló alapállásában helyesen legyen beállítva. Magát a rajzot viszont csak az eredeti, rajzoló-állásba visszaengedve vizsgáljuk meg újra, amikor a "rajzoló"-nézősugár (nr ) ismét merőleges lesz a rajz-síkra (Rs ).
Bár a tábla-emelésnél a kétféle nézősugárhoz tartozó forgatási középpont nem fedi egymást, (a fejünk a nyakon, táblát tartó kezünk a vállon át mozdul, mely utóbbit a csuklónk még korrigál); az ebből származtatható kismértékű pontatlanság, szabadkézi műfajunkban, elhanyagolható. (Kr @ Km ). |
| |
4. eset (terem-belső alsó sarka, távoli rálátás - hasonlít az 1. esethez): Hibás mérőképsík-beállításból jelentős ferdülés-torzulás származik, hasonlóan a helytelen rajztábla-sík tartásából eredő vonalhossz- tévedésekhez (b > a), ahol
a = a mérő-képsíkban helyesen beállított mérőág-hossza
b = a rajztábla-síkban "felejtett" mérőág hossza. |
|
Minél távolabb esik a mérendő ferde a rajzoló alapállásban hagyott rajztáblájától, annál nagyobb lesz a téves mérőképsík-tartás okozta mérés-különbség tartománya.
Feltétlenül figyelmeztessük azokat a diákokat a mérő-képsík helyes beállításának fontosságára, akik hajlamosak rajztáblájukat laposan elfektetn! |
|
|
|
2.3.9. A TOVÁBBFEJLESZTÉS LEHETŐSÉGEIRŐL |
|
Elképzelhető olyan speciális " tanuló-készlet " is, amely a rajztábla és egy (vagy több) mérőág összeépítéséből áll. |
|
|
Legtöbbet az a változat tudná, amelynél a rajztábla felső pereme kétirányba meghosszabbítható, skála- beosztásos sínnel egészül ki. E kihajtható mércéket függőleges állásban képsík-keretként is lehet használni. A kihúzható ágak tőcsuklója a tábla-perem mögötti sínen mozogna, vagy egyet-egyet a perem két szélső pontjára, állandó csuklós befogással rögzítenénk. Lehetne olyan perem-sínt konstruálni, amelyen egymástól függetlenül egy-egy mono ágat mozgatnánk.
Alálátások ferdéinek talpvonalig történő meghosszabbításánál jó hasznát vehetnénk egy skála-beosztásos felsőperem-sínnek, amely mindkét oldalra kihúzható. Ennek bármely pontjáról indíthatnánk mérőágat - így, akár az iránypontig is, elvezetne a megnagyobbított hasonló háromszög "talp-nyújtása". Az emelhető peremű rajzbak használata is eredményes, mivel általa a távoli alálátások vizsgálatához tartozó alapvonal-emelés mozdulata könnyen megvalósítható. (A Tanszék egyik rajztermét esténként a Műegyetemi Szimfonikusok próbateremnek használják; itt tárolják a zenekar kotta-állványait. A diákok gyakran rajztáblájuk helyett kotta-állványról dolgoznak!) |
|
|
KÉPSÍK-FÉLKERETNYI FELCSAPHATÓ MÉRCÉK |
| |
Az aránymérő első prototípusával való kísérletezés során kiderült, hogy leggyakrabban a rajztábla felső két sarkára rögzített mérőállást használják a diákok - innen kiindulva építik fel mérő-képsíkukon az aránymérés hasonló háromszögét. Nehézkes viszont a képsík-széli skála-leolvasás, hacsak nem készítenek saját mérce-csíkokat. |
| |
Innen egy lépés vezet a teljes kerületű képsíkig, amelynek pereme biztonságos támasztékot (és a befogók végpontjainál jelölhető felületet) nyújt a mérőágaknak A próbák szerint legnépszerűbb az a ferde-mérő módszer, amely fix rajztáblával is hatékony.
A vázlat egy "collstock"-szerűen kinyitható és összecsukható perem-vonalzó-sort mutat be. Ebben a változatban egyszerű kivitelű vonal-ágakkal kísérletezem. A keménypapír-sáv felső élével mérem be a ferde-közeli párhuzamosakat. Nyilvánvaló, hogy a csíkok túl sokat "takarnak" - nem mondhatok le a vonal-vékony segédegyenesekről!
Az eddigiek kombinációjaként elképzelhető a rajztábla síkjából részlegese kihajtható skála-beosztásos keret, amelynél a peremek menti talppont-rögzítést sín-, mágnes- vagy csipesz-kapcsolat biztosítja a készlethez tartozó (háromágú vagy több egyágú) aránymérővel . |
|
|
| |
ALAPFOKÚ TANULÓ KÉSZLET |
| |
A képsík széleire skála-beosztással vagy lyuk-sorral ellátott mércék hajthatók ki. A rajztábla felső pereme U-alakú metszettel készül, amelyben egy-egy pár teleszkópikus mérőág - a sarok-talppontok alapállásából egy belső sínen elmozdíthatóan - foglal helyet. Ez a "távlatrajz-tanuló-készlet", néhány további aránymérővel kiegészítve (amelyeket az oldal-peremekről indíthatnánk), a képsíkon megjelenő bármely ferdét követni tudja.
A mércék arány-leolvasását az előfúrt lyukakba betűzhető, színes gombok segítenék. Ugyanezen gombokkal az arány egész számokból képezendő számlálóját és nevezőjét is kirakhatjuk.
Felváltható a képsík-széli skála olyan mérő-beosztásos (rovátkolt, vagy színezett, mint a "Marokkó"-nevű társasjáték pálcikája) - teleszkópikus rúd-párral, amelyet csuklós gyűrűk kapcsolnak az alap-sínhez.
A befogók adatai részben a vízszintes skálán, részben a kihúzott függőleges mércén pontosan leolvashatóak.
A vízszintes képsík-peremen egy mozgó-skálát lehet alkalmazni, melynek kezdőpontját a változó talp-ponthoz igazítanánk. Az alap-sín csuklós "zongorapánttal" kapcsolódik a rajztábla-síkhoz, hiszen a készülék a megfigyelő nézősugarára merőleges mérő-képsík beállítását igényli. |
|
| 3. KÖVETKEZTETÉSEK |
|
A távlatrajz szerkezetének tanításában, szélsőségesen sarkítva, kétféle korrigálási módszert ismerünk. Az egyik szerint az " erőszakos tanár ", a diák helyére ülve, alaposan belejavít és saját kezűleg módosítja a perspektíva szabályai ellen elkövetett tévedéseket. Ezek a típushibák többnyire tévesen megbecsült "rálátások-alálátások"; tehát alapjelenséghez tartozó hiányosságokra vezethetők vissza.
A másik véglet: az " erőtlen tanár ", aki a diák válla fölött kritizál. Azt mondja például, hogy "rossz, mert nem elég ferde az eresz..." De mennyi az a "nem elég "? Esetleg mutatja is, amit mond s a levegőben - a rajz felett módosítja a hibás vonalat. (A fenti utcarajz-példánál maradva: a legfelső párkány - általában nem kellőképpen megdöntött - lejtését.)
A rajzoló nézőpontjával mindenképpen illik azonosulnia annak, aki tárgyilagosan akar távlat-rajzot kritizálni, hiszen a centrális vetítés alapelve szerint, a képsík és a szem közötti viszony a képet jelentősen befolyásolja.
Minden oktató maga válassza ki az "egyedül üdvözítő" módszert - valahol a két véglet között. Ez mindig idő, hely, alkalom, a résztvevő személyek, azok előképzettsége és még sok más tényező függvénye.
A "kezdő" rajzos igényli - és megérdemli - az objektív kritikát. A diák akkor hagyja magát meggyőzni, ha a tanár nemcsak hozzávetőlegesen mutat rá tévedéseire, hanem egyúttal ráébreszti a javítás pontos módszerére is! A rajzgyakorlaton a tanítvány azonnali, egyszerű, látványos és biztos módszert, - afféle ökölszabályt, kész receptet - vár el tanárától.
Új módszertani megközelítésemmel a szerkezeti alapvonal-háló rajzolási sorrendjének egy fontos mozzanatát "merevítem ki"- azaz a megfigyelés idejére állóképpé alakítom a távlati hatásért leginkább felelős alá- és rálátások ferdéit.
Az "arányméréses" módszert kollégáimnak demonstrációs eljárásként ajánlom, mint egyféle átmenetet a szélsőséges módszerek fent idézett végletei között: amely ugyan kevesebb, mint a "belerajzolás", de jóval több, mint a "belebeszélés". Diákjaimnak pedig (zsebben hordható) rajzolási segédeszközként kínálom fel az aránymérőt , amely megszerzi a a tárgyilagos önellenőrzés sikerélményét.
A bemutató-órák kísérletei bebizonyították, hogy az "arányméréses" módszer igen alkalmas az összetartás-rövidülés ellenőrzésére, a megfigyelés célterületeinek tudatosítására, az alapvonal-háló "ferdéinek" felbontására, a kinagyított befogók pontos összehasonlítására. Az eljárás segédeszköze a képkivágás kikeresésében, az iránypontok (esetenként rajzlapon kívüli) meghatározásában is használhatónak bizonyult. A rajzon belüli egyenesek kifelé meghosszabbíthatók - a rövid szakaszok megnagyobbíthatók. Az aránymérő segítségével további összemetsződések is felfedezhetők.
Demonstrálni lehet vele a távlat-kifejező tiszta vonalháló összes ismérvét. Szerepe van bonyolult kontúrok egyszerűsítésénél, fontos pontok meghatározásában, egyenesek helyettesítésében, sőt, tengelyek beazonosításában is.
Az aránymérő ágainak beállításával kézzelfoghatóan kijelöljük, és ezáltal tudatosítjuk a szabadkézi távlatrajzban elengedhetetlenül szükséges torzultság-mérésekhez legelőnyösebben használható a "mérő-képsíkunk" helyzetét is. Bemutatjuk az "irányba-ültetést", hiszen az eszköz használata feltétlenül kijelöli a rajzoló "felezősíkját" is.
A megfigyelés és a rajzolás fentiekben ismertetett, képsík-felbontásos módszere egyféle sorrendiségére nevel - akár az önellenőrző, akár a demonstráló oldaláról vizsgáljuk az eszközt. A tanár a leggyengébb diákot is - akár rajzának érintése nélkül - rá tudja vezetni a távlat alap-jelenségeinek felismerésére, amikor a tanítványának helyéről nyíló nézőpontból készre állítja a mértékadó ferdék helyzetét rögzítő mérőágakat.
A felsorolt indokok alapján az általános szerkezeti típushibák tévedéseinek eredményesebb felszámolásában számítok újszerű eljárásom segítségére.
A perspektíva-szerkesztés eddig kitalált segédeszközei vagy túl egyszerűek, vagy túl bonyolultak voltak ahhoz, hogy igazán használhatóak legyenek a mi gyakorlatunkban. (7)
A legtöbb energiát a vetületekből helyreállítandó perspektívák gépesítésébe fektették - amíg a számítógép színre nem lépett.
Új módszertani megközelítésem oktatási segédeszközét eredetileg gyakorlati eszköznek szántam, mellyel a problematikus, kezdő diákok látás-tanítását kívántam felgyorsítani. Az első kísérletek visszaigazolták, hogy alapvető elméleti fogalmak magyarázására is jól használható.
A szabadkézi rajz kevés eszközt igényel - ezeket egészítené ki, a tanulás kezdetén, az aránymérő . Oktatói szerepe a bemutató-jellegű rávezetésben, a megfigyelendők gyakoroltatásában, egyszóval a látás tanításában rejlik. A kezdő tarsolyában - a sok, jól kihegyezett ceruza mellett - legyen egy-két aránymérő is!
A tanítványok többsége hamar túljut az "aránymérés" segédeszközzel támogatott kezdeti fokán. Néhány próba elegendőnek látszik kitűzött oktatási céljaink eléréséhez. Minél gyorsabban érik el ezt a küszöb-szintet, annál hamarabb túl is léphetnek felette; hiszen, elsajátítván az alapvonal-háló helyes ábrázolásának feltétel-rendszerét, szilárd alapokra építhetik - egyéb eszközökkel tovább gazdagítandó - rajztudásukat.
Meggyőződésem, hogy a saját szemmértéket semmi sem helyettesítheti - viszont annak kifejlesztésére minden, eredménnyel kecsegtető módszer bevezetése megengedhető. |
|
ÖSSZEFOGLALÁS |
|
Az építészeti szabadkézi rajz szerkezeti felépítésének oktatásában a legtöbb gondot a helyes távlati hatás illúzió-keltésének tanítása jelenti.
A mélység látszatáért főként felelős ferde vonalak meghatározásáról, azaz a ferdék főirányokhoz képest viszonyított dőléséről van szó. A perspektíva összetartó egyenesei a "mérő-képsík" keretein belül ferdének látszó vonalakként jelennek meg. Adott nézőpontnak csak egyféle perspektivikus torzulás felelhet meg. A távlattal foglalkozó rajzok legáltalánosabb szerkezeti hibái az e tárgyban elkövetett tévedésekre vezethető vissza.
Az "arányméréses" módszertani megközelítést az építészeti szabadkézi rajzoktatás kezdeti szakaszában ajánlom bevezetésre, amikor az oktatónak feltétlenül szüksége van arra, hogy a látvány kritikus összefüggéseit - tanítványa szemszögéből vizsgálva - meggyőzően bemutassa!
Az eljáráshoz kifejlesztett segédeszközt " aránymérőnek " neveztem el. Ennek a szemmérték és arányérzék fejlesztését önellenőrzéssel támogató, a kritikai észrevételeket tárgyilagos beállítással demonstráló segédeszköznek az a szerepe, hogy a távlat síkbeli ábrázolásának mentális folyamatát néhány döntő fontosságú lépés végigkísérésével tagolja.
A rajzolás tanítható részének alap-eleme a sorrendiség .
Az " aránymérő " segítségével, a rajzoló mérő-képsíkján (amely a rajztábla felső pereméhez illeszkedik) bizonyos pontokat ill. egyeneseket ideiglenesen rögzíteni képes. A mérés úgy történik, hogy a megfigyelés célterületeit megfelelő sorrendben, az összehasonlítások, bevetítések, az " aránymérések " idejére, ezen a mérő-képsíkon beállítjuk. Aki képes virtuális képsíkjának adatait - helyesen megválasztott - arányban átvinni rajzlapjának síkjára, az megoldotta a távlati ábrázolás szerkezetének titkát.
Bár az aránymérő mindenfajta képsík-beli ferde vonal dőlés-mérésére alkalmas, elsősorban a térbeli alapvonal-háló rövidülés- és összetartás-jelenségeinek ábrázolásában, a távlat vonalas kifejezésének oktatásának kezdetén használhatjuk kézzelfogható eredményességgel. |
|
TÉZISEK |
| |
1 - ( Típushibák ) |
| |
Azt tapasztaltam, hogy természet után készített távlati képek szerkezeti hibái nagyrészt a térbeli alapvonal-háló legkritikusabb összetevőinek, a mélység-érzet kialakulásáért főként felelős ferdéknek helytelen ábrázolásából adódnak. |
| |
2 - ( Aránymérés ) |
| |
Az általam kidolgozott " arányméréses " megközelítés a látvány szerkezetének szélsőséges ferdéire koncentrál. A redukált látvány ferdének látszó egyeneseit a mérő-képsíkon kinagyítom, hogy a nézőpontomnak egyedül megfelelő dőlés-viszonyokat a perspektivikus torzulás mértékében vihessem át a rajz síkjára. |
| |
3 - ( Látásmód ) |
| |
Megállapítottam, hogy új megközelítési eljárásom ebben a folyamatban - a képmező síkidomokra való bontása révén - a megfigyelés célterületeinek tudatosításával, jelentős technikai gyorsítást eredményezett, s egyúttal sajátos látásmódra nevelte hallgatóimat. |
| |
4 - ( Az "Y" - csomópont ) |
| |
Kísérleteimmel bebizonyítottam, hogy a térbeliség arányhelyes síkbeli ábrázolásának bevezetésére kitűnően megfelel az ún. "Y"-csomópont elemzése, amely a redukált környezet alapvonal-hálójának nevezetes sarkainál elvégzendő alá- ill. rálátás-méréseket jelenti - különös tekintettel azokra az általános esetekre, amikor a vonatkozó iránypont kívül esik a képmezőn. |
| |
5 - ( Pedagógia ) |
| |
Rajzpedagógiai szempontból az arányméréses megközelítés közvetlen belerajzolás nélkül, de a szóbeli kritikánál hatékonyabban segíti a kezdő rajzosokat a szerkezeti gerincet adó tisztavonal-háló felépítésében. |
| |
6 - ( Értékelés ) |
| |
Kísérleteim szerint az arányméréssel kombinált redukciós eljárás mindkét fél (tanár, diák) számára tárgyilagosan elfogadható bizonyítékként használható a " Látandó " és a " Látott " közti esetleges vitában - s ezért az értékelésnél megfelelő pontosságú támpontot nyújtott. |
|
KULCS-SZAVAK GYŰJTEMÉNYE |
|
ALAPVONAL-HÁLÓ: a távlati rajz szerkezeti gerincét adó, főleg a kontúrokat és a térhatároló síkok metszésvonalait tartalmazó vonal-együttese, amelyet felületosztással ill. anyagjelöléssel - azaz " folt-sűrítéssel " - és egyéb grafikai kellékeinkkel öltöztetünk fel a továbbiakban. Önmagában is tér-mélységet érzékeltet.
ARÁNYMÉRÉS: A vonal-perspektíva alap-jelenségeinek (rövidülés, összetartás) oktatásában, a térbeli alapvonal-háló torzulásait mérő-képsíkunkon főleg mint egyenesek változó viszonylatait észleljük. Ezek elemzésére vonatkozó olyan módszer, amely a redukált látványt - a rajz szerkezeti felépítésének idejére - jól mérhető síkidomokra bontja és a rajzolási sorrend egyes lépéseit tudatosítja.
ÁTLÓS MÓDSZER: A tárgy- ill. térmodul felület-osztására használt négyzetháló alapegységének sokszorosítására alkalmazott egyszerű geometriai szerkesztés, amellyel akár vetületekben, akár perspektívában, egyenlő szakaszokat szaporíthatunk: a sarkot az átellenes oldal felezőpontján tükrözzük át (ld. 1.2.22.).
CERUZÁS MÉRÉS: A virtuális mérő-képsíkon megjelenő szakaszok összevetésére eddig használt (de csak hozzávetőleges eredményt adó) módszer. Lényege az, hogy a nyújtott karral kitartott ceruzára, annak tompa végétől számítva, a hüvelykujj csúsztatásával fogjuk be az aránypár részeként rögzítendő szakaszhosszat.
CENTRÁLIS VETÍTÉS: másképpen: perspektivikus ábrázolás - olyan pont-transzformáció , amelynek segítségével térbeli alakzat síkban ábrázolható. A vetítési középpontot (szemünket) a vetítősugarak (nézősugarak) révén pontonkként összekötjük az ábrázolandó alakzattal. A tárgy képét a vetítősugarak képsíkkal való metszéspontjai adják.
EGYSZERŰ GEOMETRIAI FORMÁK: Az aránymérés szempontjából egyértelműen számszerűsíthető (azaz megnevezhető) síkbeli alakzatok: számunkra ilyenek a derékszögű háromszögek és a párhuzamos oldalpárú négyszögek. Ezekre bontjuk a tiszta vonalra redukált tárgyak és terek képsíkon megjelenő foltrendszerét, hogy a kapott adatokat - megfelelő sorrendben és arányban - rendre átvihessük rajzunkra.
FELEZŐSÍK: A rajzoló hossztengelyre illesztett, a padlósíkra és a szemsíkra merőleges - képzeletbeli felület, amely a "megfigyelő-" és a "rajzoló"-nézősugarat egyaránt tartalmazza. Ezzel a síkkal célozzuk meg a téma súlypontját. A megfigyelés mérő-képsíkja és a rajzolás rajztábla-síkja szintén derékszöget zárnak be a felezősíkkal.
FŐIRÁNYOK: A térbeli főirányokat a kocka sarok-élei képviselik. A síkbeli főirányok a rajzlap két szomszédos oldalával párhuzamos egyenesek, amelyekhez a távlati kép szerkezetének "ferdéit" viszonyítjuk.
FŐMÉRETEK: Tárgy-rajznál a "befoglaló" forma körvonalának szélső pontjaira illesztett, a főirányok által közrefogott négyszög két szomszédos oldala.
IRÁNYPONT: Párhuzamos egyenes-pár látszólagos (azaz képsík-beli) metszéspontja (ez a Kepler -féle "ideális pont"). Vízszintes síkon futó párhuzamos egyenesek iránypontja a horizonton lesz. Ha a térben a képsíkunkkal is párhuzamosak ezek a vízszintes egyenesek, akkor perspektivikus képük is vízszintes marad - (iránypontjukat kétoldalt, a végtelenben képzeljük el).
KÉPPONT: A téma tárgypontjait a szem, mint centrum, a vetítő- ill. néző-sugarakkal tapogatja le. Ott, ahol a nézősugár átdöfi a képsíkot, keletkezik a tárgypontnak megfelelő képpont.
KÉPSÍK: Az a sík, amelyre az ábrázolandó alakzatot vetítjük: a távlati kép jeles pontjainak két dimenzióban való rögzítésére szolgál. A vezérsugárra merőlegesen bárhol felvehetjük. Minél közelebb érünk a szemhez, annál kisebb lesz a kép - de a torzulás arányai azonosak maradnak.
MÉRŐ-KÉPSÍK: A rajztábla felső pereméhez kapcsolódó, a "megfigyelő-nézősugárra" merőleges virtuális képsík, amelynek főirány-beli széleihez képest, arányméréskor , a ferdék dőlés-elemzését végezzük.
ÖSSZETARTÁS: A térbeli modulháló - képsíkkal nem párhuzamos - éleinek látszólagos sűrűsödése . Mértéke a szabadkézi távlatrajz szerkezetében meghatározó jelentőségű. Pontos leképezéséhez az "arányméréses" eljárást ajánlom, mely szerint a mértékadó (szélső) ferde egyenesek dőlés-helyzetét a mérő-képsíkon számszerűsítjük, és aránypár részeként visszük át rajzunkra.
RÖVIDÜLÉS: A másik legáltalánosabb perspektíva-alapjelenség: a térháló négyzetosztásait sűrűsödő közök szövedékeként észleljük a képsíkunkon.
VETÜLETEK: A ( Monge -féle) párhuzamos vetítés során keletkeznek, ahol a képsíkok egymásra merőlegesek.
VEZÉRSUGÁR: A perspektívában leképezendő tárgy súlypontja és a rajzoló szeme közötti legrövidebb távolság.
VEZÉRSÍK: A mérő-képsíkkal párhuzamos felület, amelyen a főirányok hálózata még nem torzul. Ilyen pl. a rajzolóval szemközti fal osztás-rendje. A függőleges és vízszintes skála arányhelyes felvételét ezen a mérőhelyen javaslom elkezdeni. |
|
IRODALOMJEGYZÉK |
|
1 - YVES DEFORGE: LE GRAPHISME TECHNIQUE - SON HISTOIRE ET SON ENSEIGNEMENT
(Champvallon, 1981)
2 - PIERRE DESCARGUES: TRAITÉS DE PERSPECTIVE
(Edition Ste Nille du Chene, Paris, 1976)
3 - BETTY EDWARDS: AT TEGNE ER AT SE - INDFØRING I FRIHANDSTEGNING
(Nyt Nordisk Forlag Arnold Busck, København, 1982)
4 - FENYŐ IVÁN: DÜRER
(Képzőművészeti Alap Kiadó Vállalata, Bp. 1955)
5 - R.G.HATTON: Perspective for Art Students
(London, 1903. Chapman and Hall)
6 - ERIC JANTZEN: TRAITÉ PRATIQUE DE PERSPECTIVE
(Edition de la Villette, Paris, 1983)
7 - JEAN-PAUL JUNGMANN: OMBRES ET LUMIERES
(Les Editions de la Villette, Paris, 1991)
8 - MÉHES BALÁZS: ILLUSTRATED DRAWING OF CUBIC FORMS
(Periodica Polytechnica, Bp. 1985);
9 - MÉHES BALÁZS: A VÁROSKÉP ÉS AZ ÉPÍTETT JEL KAPCSOLATA
(Doktori Értekezés, Budapesti Műszaki Egyetem, 1993)
10 - KIMON NICOLAÏDES: TEGN PÅ DEN NATURLIGE MÅDE - EN ARBEJDSPLAN TIL SELVSTUDIUM
(Borgens forlag, 1977)
11 - TERMÉSZETTUDOMÁNYI LEXIKON
(Akadémiai Kiadó, Budapest, 1968)
12 - G. SCHAARWACHTER: PERSPECTIVE FÜR ARCHITEKTEN
(Verlag A. Niggli - Teufen, 1964.)
13 - LAWRENCE WRIGHT: PERSPECTIVE IN PERSPECTIVE
(Routledge and Kegan Paul, London, 1983)
14 - TH.C.WHANG: PROJECTION DRAWING
(Yan Nostrand Reinhold Comp., New York, 1984) |
|
FÜGGELÉK |
|
FELJEGYZÉSEIM AZ ELSŐ ARÁNYMÉRÉSES KÍSÉRLETEKRŐL |
|
A - ANGOLNYELVŰ I. ÉVES ÓRA (1996. nov. 28.)
|
| (A PROTOTÍPUS TANULSÁGAI) |
| |
(1) A diákok annyira magától értetődőnek tartják a "ferde-fogó" ( PROPORTION HOLDER ) alkalmazását, hogy megkérdezik: lehet-e már üzletben kapni?
(2) Most derült ki, hogy a mérendő ferdét nem szükséges közvetlenül ráilleszteni a képsík-beli ferdére - egy közeli párhuzamos beállítása is megfelel a célnak!
(3) A továbbfejlesztés csírája lehetne: a rajztábla felső peremének - kihúzható sín formájában való - meghosszabbítása (2.3.9.).
(4) A befogó-méréseket a képsík széléig megnagyobbított hasonló háromszögekben egyszerűbb elvégezni, mint a belső mezők (kicsiny) látvány-foltjain - ott, ahol a "ceruzás-mérés" bonyolódik.
(5) A befogó-méretek rajztábla-széli leolvasására keménypapír-csíkokat alkalmaztunk, melyeket a felső sarkok csuklói körül (collstock-szerűen) kihajtogatunk.
(6) Azt mérlegeljük a diákokkal, hogy érdemes-e törődni a rajztáblasík / mérőképsík közti szögbeállítással, ha az ellenőrzéshez megemeljük a rajztábla peremét? Az elméleti demonstráció miatt feltétlenül be kell állítani a "megfigyelő"-nézősugárra merőleges saját mérő-képsíkunkat - ehhez pedig szükség van az eszköz ágainak "felezősíkban" való negyedkörnyi forgathatóságra (2.3.8.). |
|
B - NÉMETNYELVŰ I. ÉVES MÉRNÖKCSOPORT (1996. december 4.) |
| |
(1) Az értékelésnél nemcsak a "mérés" számít, hanem a teljes munka összképe is!
(2) Együtt ellenőrizzük az eszköz segítségével a szögletes testek térbeli négyzethálóját, különös tekintettel a "hátsó" lapok látszólagos torzulásának a helyességére.
(3) Az előre meghirdetett helyen lebonyolított "aránymérés" objektíven rögzíti a tényleges perspektívikus torzultságot a diákok szeme láttára. Mennyire látszik a valóság vízszintes egyenese - a hallgató képsíkján, az ő nézőpontjából szemlélve - "ferdének"?
(4) A szabadkézi rajz szerkezeti felépítésének időrendjében jól körülhatárolható szakasz a mértékadó ferdék dőlés-mérése. Tapasztalatom szerint ez a közbülső lépés a távlatrajz tovább-építhetőségének egyik fontos feltétele. |
|
| C - ANGOLNYELVŰ I. ÉVES ÉPÍTÉSZ-CSOPORT (1996. december 5.) |
| |
(1) Az alapvonal-háló felrajzolásában elkövetett tragikus tévedések dacára mégis látszik a továbblépés lehetősége, mert a segédeszköz mintapéldányát érdeklődéssel fogadják. Még a leggyengébb diákot is meg tudom győzni új demonstrációs módszeremmel, hogy a "távolodó él" ferdéjét jobban billentse meg!
(2) Bizonyos hallgatói csoportok alaphibája az, hogy nem éreznek különbséget a párhuzamos és az általános (vagyis a képsíkkal nem párhuzamos térhálójú) beállítás között. Ezért képtelenek "eléggé ferdének" ábrázolni a távlati kép szerkezeti hálójának összetartó egyeneseit - amelyeknek pontos mértékű dőlése ezzel a megközelítéssel taníthatóbbá válik.
(3) Ha már kellő eredményt értünk el a távlati kép gerincét adó alapvonal-hálóval, felsorakoztathatjuk egyéb , térhatást-fokozó eszközeinket: a tárgyak és környezetük felület-osztását, anyagjelölését, az árnyékokat és a színeket is.
(4) Ezt mindenképpen előzze meg a vonalak grafikai játékával történő távlat-kifejezés tanítása (pl. a vonalvastag ság változtatása, felületek folt-hatása, vonalkázások, a síkok négyzethálójának kiterjesztése, stb.). |
|
| D - KIEGÉSZÍTŐ KÉPZÉS I. ÉVF (1996.dec.12.) |
| |
(A KÉPSÍK-KERETES ARÁNYMÉRŐ KIPRÓBÁLÁSA) |
| |
(1) A módszer fontos része a befogók hányadosának megállapítása. A gyakorlatok során különféle rögtönzött mérőlécekkel próbálkoztunk: pontos skála-beosztást a képsík-keret belső élein lehet létrehozni.
(2) A képsík-keret a képkivágás kompozíciójának a kiválasztásában is szerepet kap, a felesleges környezeti sávok kitakarásával a lényegre való koncentrálást segíti elő.
(3) A képsík-keret beállításánál arra ügyeljünk, hogy a rajzolandó tárgycsoport, ill. tér-részlet függőlegesei a keret függőleges széleivel legyenek párhuzamosak: így lesz a megfigyelő-nézősugár a mérő-képsíkra merőleges. Ezzel a keret használata a helyes "irányba-ülést" és rajztábla-tartást tudatosítja.
(4) A gyakorlat közben elegendőnek bizonyult a mértékadó ferdék "pálcás" rögzítése, a többi ferde viszonyát a másik kézben tartott pálcával mértük. |
|
| E - EGY ÚJABB PRÓBA (1977. január 22.) |
| |
(1) A helyes megoldás aránymérővel való bemutatása "megváltás" a tárgyak sorolásával kínlódó diáknak (a padló négyzethálójából "kilógnak" a váz-testek!). Tipikus eset, hogy "nem akarnak összeérni a körvonalak..." pedig tárgyról-tárgyra haladva, egyenként meg tudott birkózni a diák az egyes elemekkel (nem a nézőpontjának megfelelő torzítást rajzolta).
(2) Jellegzetes hiba az is, amikor csak a "pozitív" tömegeket látja a hallgató, s a köztük levő tér-hiányt nem érzékeli.
(3) Nem minden "ferdére" illeszthető közvetlenül az aránymérő ága. A "ferde-közeli párhuzamos" beállítása bizonyos gyakorlatot, szemmértékkel való elő-becslést követel.
(4) Mindig lehet - a diákkal közösen - olyan ferdét találni, amelyik meghosszabbítva a mérő-képsík peremét döfi (pl. a padló-négyzetek átlói). |
|
| F - A MONO-VÁLTOZAT HASZNÁLATÁNAK TANULSÁGAI (1997. február 5.) |
| |
(1) A függőlegesek ellenőrzésénél alkalmazandó (ceruzahossznál nagyobb) oldaltávolságok mérésére is beválik a segédeszköz, hiszen a rajztábla átellenes pereméig is átérünk vele!
(2) Általános kezdőpontnak - talppontnak - igen alkalmas a rajztábla felső két sarka.
(3) A kihúzott mérőágat pálcaként emelve, a rajztáblán kívül eső iránypontba összetartó sugárnyaláb ellenőrzésére is használható. Meghosszabbított vonalzó - ill. mutatópálca - van így a kezünk ügyében.
(4) Könnyű vele a látszólagos tengely-ferdüléseket bemutatni.
(5) Mérési talppontot a virtuális ferde meghosszabbításával jelölhetünk ki. |
|
| G - A FRANCIAORSZÁGI BEMUTATÓ TAPASZTALATAI (Strasbourg, 1997. május 14.) |
| |
| (1) |
Az Ecole d'Architecture de Strasbourg első- és másodévesei hallgatóinak, a "Croquis Urbains" c. tárgy keretén belül, az Iskola amfiteátrumában rendezett előadásommal sikerrel mutattam be az "arányméréses" új megközelítést.
Az ismertetés elején kiosztom a jelenlévőknek a segédeszköz minta-példányait, amelyek kézről-kézre járnak. Írásvetítővel transzparenseket vetítek: Hogyan kell a mérő-képsíkot használni; miért koncentrálunk a szerkezeti felépítés fázisában a "ferdének" látszó egyenesek helyes megfogására, stb.
A táblát helyettesítő fehér fal-lemezre fekete filctollal rajzolok: a vonal-perspektíva alapjelenségeit és ezek vonalra gyakorolt hatását magyarázom.
Előző elméleti órájuk anyagára támaszkodva (amikor Mme Valery NEGRE a "Dessin d'Architecture" témakörben híres elődök színes látványterveit vetítette) hangsúlyozom a távlati kép szerkezetének szükségességét. A gondolatmenet lánc-szemei: vetement - sous-vetement - peau - muscle - ossature. Csak az egészséges váz-szerkezet biztosítja a későbbi dísz-ruházat felöltésének lehetőségét!
A tanár-kollégák kérésére (Laurence Reynes, Michel Danner, Madame Pollet) előadásom szövegét az Iskola könyvtárában letétbe helyezem. ("UNE NOUVELLE APPROCHE METHODOLOGIQUE D'ENSEIGNEMENT DE LA STRUCTURE DU DESSIN ARCHITECTURAL A MAIN LEVEE") |
|
| |
(2) Az előadást követő rajz-gyakorlat teljes elismerést hozott az újszerű módszertani megközelítés számára. (Helyszín: az Observatoire a Füvészkertben.) |
| |
| |
A bonyolult belső térben nagyon nehéz behatárolni a látványt. (Kör alaprajz, kupolával fedett henger - a bordák rácsostartók, mint a földgömb szélességi és hosszúságú körei! A kupola-nyíláshoz küllős kerekek és görgők tartoznak a derék-sávban. A parketta bonyolult intarzia-mintával van kirakva. Jules Verne -féle hangulat: klasszikus térben nemes anyagok találkoznak a gépkorszakkal.)
A tér középtengelyében egy vaskos acéloszlop tartja a távcsövek és többszörös ellensúlyok (megannyi kitérő egyenes!) csillagvizsgáló-szerkezetét.
Külön ábrázolási probléma a belső héjra vetett borda-árnyékok rendszere. Nehéz megtalálni a viszonyítási pontokat (Points de reperes), mivel a gépezettel telezsúfolt, zárt térben túl sok a látnivaló.
Az oktatók krokikat kérnek - a henger és a gömb belülről való ábrázolása a diákoknak nagyon nehezen sikerül. Én velük rajzolok.
Kiindulásul a lépcsőkar lejtőjét használom fel, amely ferdeszöget zár be az objektív vetített képét felfogó csillagász-asztal állványzatának ferdéjével. Az említett ferde vonalak az " arányméréses " módszer szerint mérhető részét képezik a látvány szerkezetének; a háttér további jeles pontjait majd a középtér rács-szerű alkotóelemeihez viszonyítom. |
|
|
| |
(3)
(4)
(5)
(6)
(7)
(8)
(9) |
A belső tér rajzolása után kívülről tanulmányozom a kupolát. A Jardin Botanique közepén emelkedő épület kereszthajós bazilika-tömegére nyolc-szögletű terasz került. A homorú sarokban találom meg azt a "vezérsíkot", amely a perspektíva szerkezeti vázának indításához szükséges. A függőleges skálát a szemben lévő falsík kőosztása adja. A terasz-peremek alálátásos "ferdéit" ettől kezdve ehhez a rendszerhez igazítom.
A rajz főtémájának méltó ellenpontja a favázas kerti pavilon pergola-gúlája, amely szintén nyolc-szögletű hasáb. A kupola-kontúr ívét - a kör-perem megrajzolása után - pontonként emelem ki. Most válik érthetővé a félgömbök határánál az a két egységnyi, vastagabb borda-perem, amely a Csillagvizsgáló sziluettjének jellegzetessége.
Véleményem szerint az épület-elemzést kívülről kellett volna kezdeni; s az összetett formák tanulmányozását bent folytatni, ahol a tárgy-távolság leszűkül.
A diákok reakciója nagyon közvetlen: "Ça se vend, votre truck?" ("Ez a valami már kapható?") Újra elmagyarázom, hogyan működik a segédeszköz: hol van a talppont, miért kell a "mérő-képsíkban" mozgatni a mérőágat, stb.
Mivel az eszköz elsősorban az ő munkájukat könnyítené meg, gyorsan megértik az újszerű megközelítés nyilvánvaló előnyeit.
A gyakorlati mérésnél gondot jelent az, hogy szinte senkinek sincs klasszikus rajztáblája (csak rajztartó-mappája, amelyet alátétként is használnak), mindenki blokkra rajzol. A vékony és rövid felső-peremek ezért kiegészítő alátét-elemet kívánnak, hogy a segédeszközt feltűzhessük. Itt egy keskenyebb talp-csipesszel ellátott mérce lenne kelendő.
A diákok elemi problémákkal küszködnek (ami a vonalperspektíva alapjelenségeit illeti), s ez visszavezethető arra a tényre, hogy csak egyetlen (4 órás) alkalommal rajzoltak "szögletes testeket". Hiányzik az elemző alapozás! (Pl. összekeverik az alá- és rálátást, nehezen találják meg a szemsíkot, elvesznek a részletekben, kifordítják a homorú felületet - nem tudják a térbeli tárgyakat egymáshoz viszonyítani, stb.)
Alkalmi társ-korrektorként az ívek kiváltásával, a körök négyzetekbe írásával, a ferde-síkok térhálóra-illesztésével segítek nekik. |
|
|
|
|
MELLÉKLETEK |
| |
| I - AZ ARÁNYMÉRŐ MÓDSZERTANI SEGÉDESZKÖZ LEÍRÁSA |
| |
| |
Ez az Építészeti Műleírás jellegű rész Sóvári Miklós szabadalmi ügyvivő úr részére készült, 1997. január 4-én (Danubia). A tényleges szabadalmi bejelentés (P9700483) szakszerű szövege az ő munkája. |
|
| |
Kulcs-szavak: alapvonal-háló, aránymérés, ceruzás mérés, felezősík, főirányok, mérő-képsík, mértékadó ferde, megfigyelő- ill. rajzoló-nézősugár. |
| |
1.
2.
3.
4.
5.
6.
7. |
Bevezetésének indoklása: Az iránypontok általában nincsenek a rajzon. A gyakorlatban a rövidülések ferdéivel van dolgunk. A típushibák a rálátás ill. alálátás helytelen felvételére vezethetőek vissza. A perspektivikus ábrázolásban az ARÁNYMÉRŐ a ferde egyenesek képében megjelenő rövidülések ill. összetartások pontosabb megfigyelésére és tárgyilagosabb ellenőrzésére alkalmas.
Alkalmazásának javasolt ideje: A perspektíva oktatásának kezdeti szakaszában, amikor az egyszerű tárgyak, tömegek ill. terek ábrázolását oktatjuk. A tiszta vonalrajzra redukált távlati kép mélységi hatásáért főleg a ferde vonalak felelősek. A ferdéket a képsík széleihez viszonyítva, azaz a függőleges és vízszintes főirányokhoz képest érezzük ferdének. Ezek gondos megfigyelése, a ferdeség mértékének pontos megállapítása döntő jelentőségű a rajzoktatás alapozó periódusában, a perspektíva-rajz szerkezeti gerincét alkotó alapvonal-háló felépítésében.
Erényei: Egyrészt az oktatásban - a diák "erőszakos belerajzolás" nélkül és egyértelműen meggyőzhető a látvány-részlet torzulásáról - hiszen visszaülve a tanár által az ő helyén demonstrált mérőág-beállításhoz, felülvizsgálhatja a bírálatot;
Másrészt az önálló rajzolásban - a zsebben hordható ARÁNYMÉRŐ az önellenőrzés hatékony eszközévé válhat: pl. utcarajznál a "mértékadó" ereszalálátások meredekségét pillanatnyi képsík-rögzítéssel megfoghatóvá teszi.
Részei:
A - MÉRŐÁG: változtatható hosszúságú és - a vízszinteshez képest - változtatható szögben beállítható, vonalszerű, vékony pálca;
B - CSIPESZ: amellyel a rajztábla felső peremén, azaz a "mérő-képsík" alján, egy megfelelően kiválasztott talppont-helyen rögzíthető a mérőág;
C - TŐCSUKLÓ: amely a kétirányú mozgathatóságot szolgálja: a virtuális mérő-képsíkon való mozgatás (max. 180 o ) beállítása előtt az ARÁNYMÉRŐT merőlegesre kell állítani a "megfigyelő nézősugárra". A mozgathatóság mértéke itt max. 90 o . (A rajztábla síkja pedig a "rajzoló-szemsugárhoz" képest legyen derékszögű.)
Használata: A ferdeség mértékét az egybevágó háromszögek hasonlósága alapján, a befogók összevetésével határozzuk meg. A mérendő ferde (mint átfogó) főirányokba bontott vetületeinek (mint befogóknak) hányadosa a tudatosítandó arányszám , amelyet a rajzoló, a mérő-képsíkjáról leolvasva, rajzára alkalmaz.
(Fontos megjegyezni, hogy nem abszolút értékeket másolunk, hanem a mért befogók arányát! A kapott eredmény a kiindulásul választott kezdőszakasz méretéhez fog igazodni, melyet a rajzfelület felosztása során kialakított " befoglaló forma " határoz meg, tehát aránypárokkal dolgozunk.)
A mértékadó ferde dőlésének megállapításához az ARÁNYMÉRŐ tőcsipeszét a rajztábla felső peremének megfelelő pontjára rögzítjük, majd a mérőágat fedésbe hozzuk a ferdével. Ha túlzott mértékű tábla-mozgatást igényelve ez a művelet, akkor egy ferde-közeli párhuzamost állítunk be.
Az így kapott átfogót a képsík széléig meghosszabbítjuk: a mérő-képsík szélei a rajztábla szélességével essenek egybe. A kinagyított, "nagy-háromszög" befogóin most már tetszőlegesen választott helyen olvashatjuk le a befogó-arányt. (Célszerű pl. a kézben tartott ceruza hosszához, mint "egységhez" mérni a másik befogó hosszát).
Emlékeztető a korábbi módszerekre: nyújtott karral, kézben fogott ceruzával próbáltunk szakaszokat egymáshoz hasonlítani, ill. a ferdéket "párhuzamosan lecsúsztatni". Ezek a "ceruzás" mérések pontatlanok, mivel a kartávolságban elképzelt képsíkon megjelenő részletek kicsinyek; a mérés elemeinek egymáshoz való viszonya bizonytalan.
Alkalmazásának korlátai: csak a körülírt oktatási szakaszban szemléltessünk az eszközzel - a ferde-mérés módszereként, a rajzolási sorrend tanításában, a képmező síkidomokra való bontásához. Nem szabad hátráltatnia az önálló szemmértékkel való szabadkézi rajzolást. |
|
| |
Hivatkozások az eszköz szakirodalombeli elődeire: |
| |
Eddig főleg a vetületekből való perspektíva-visszaállítások szerkesztéséhez találtak ki segédeszközöket. Ilyen volt pl. az Y-alakú, távoli iránypontokra specializált vonalzó ("centrolinead"); a háromszögletű, konkáv-peremű rajztábla ("kalibrált centrolinead"); vagy H.W.Robert (1912) mm-beosztású perspektíva-grafikai papírja; id. Thomas Malton pantograph-ja; C.W.English (1900) pontozógépe; ill. a Meredith -féle projektor (ahol a vetítőlámpa volt a nézőpont). |
| |
Forrás: LAWRENCE WRIGHT, PERSPECTIVE IN PERSPECTIVE
(Routledge and Kegan Paul, London, 1983. 358. oldal). |
|
A színpad-építészetben használatos a Lamberth -féle "perspektográf" (állványos, üveglapos, fix nézőponttal), melyet 1752-ben szerkesztett Victor von Ranke . |
| |
Forrás: G. SCHAARWACHTER: PERSPEKTIVE FÜR ARCHITEKTEN
(Verlag A. Niggli-Teufen, 1964.) |
| |
| A másik út, amikor a látvány szerint készül a távlati kép - ehhez elsősorban Dürer művészetelméleti írásai nyújtanak fogódzót (vezérsugár, képsík, nagyítás ... a lantrajzolót, akt-rajzolót ábrázoló fametszetei a "Perspektíva és Arány" c. művéből, 1525). |
|
Forrás: FENYŐ IVÁN: DÜRER
(Képzőműv. Alap Kiadóváll. Bp.1955. 84.o.) |
|
|
|
| II. EGY BELSŐ TÉR RAJZOLÁSÁNAK ELEMZÉSE - A "DUNA-PLAZA" |
| "A puding próbája az evés" |
|
|
|
Hogyan tudom valóságos szabadkézi távlatrajzon új módszertani megközelítésemet alkalmazni?
A "Duna-Plaza" (Budapest, XIII. Váci út 197.) bevásárló központ igen alkalmas helyszín a térbeli ferdék rajzolásához. Tört vonalvezetésű belső utcák, hidak és folyosók fedett, többszintes átriumban futnak össze.
Sokféle érdekes nézőpontból választhatunk témát - rajzommal a központi tér III. emeletének függőfolyosó-korlátjánál állva tekintek a Mozik belső utcája felé. Ez a nézet egyaránt tartalmaz "egy-iránypontos" utcafal-rövidüléseket és "két-iránypontos" ferdéket is: a központi tér kerületének hídjait és folyosóit.
Az egy-iránypontos rész összetartó ferdéinek enyészpontját hamar megtalálni a rajzfelület középtáján. Az utcatengelyhez tompaszöggel kapcsolódó belső udvar ferdéinek iránypontjai a rajzon kívül esnek. A középrész alaprajza háromszöggel bővített négyzet, a földszinten kör alakú jégpálya van . |
|
|
(A)
(B)
(C)
(D)
(E)
(F)
|
A választott tus-technika miatt a belülről - kifelé való, részletről-részletre építés módszerét követem, vagyis a " befoglaló formát " felvázoló mozdulat a levegőben történik.
Foltonként rajzolom a III. emelet két közeli oszlopa között nyíló, trapéz alakú látványt.
A szemben levő " vezérsík " - amelyen a függőleges- vízszintes méretek még torzulásmentesen mérhetők - a háromszintes, belső utca "rövid" fala lesz.
A vezérsík szélén, az üvegfal négyzet-osztásos háromszögénél kezdem szőni vonalhálómat.
Mi fér bele a látó-kúpba? A teljes rajzfelület és az ábrázolandó látvány arányában előre meg kell határozni a vezérsík foltjának hozzávetőleges helyét. (Az előzetes folt-elhelyezés történhet ceruzával is.)
A leghátsó üvegfal rács-osztása szabályos négyzetháló - a nyeregtető üvegosztása viszont már rövidülésben látszik. Nézőpontom helyi különlegessége az, hogy a központi aula (trapéz) szemöldöke hogyan metsz az üvegfal osztás-rendszerébe? Itt már egymást hegyesszögben metsző egyenesekkel van dolgom, hiszen az utca végfalának a síkja nem párhuzamos a hídfal síkjával. Ezért lesz az üvegfal háromszögéből sokszög . A sokszög alakját a határoló ferdék vízszinteshez viszonyított helyzetével állapítom meg. |
|
| |
A rácsosztást szemből látom: ezért ez a háló - a folt-építés kiinduló moduljaként - mérhető. A rövidülésben látszó nyeregtető sűrű üvegosztása a sarokjelnél határolja a kezdő négyzethálót. Belső terek rajzolásánál - ha van szemközti fal - kezdjük a munkát a vezérsíknál! |
|
|
(G)
(H)
(I)
(J)
(K)
(L) |
Fentről-lefelé folytatom a belső utca jobb-hátsó sarok-élének rajzát, annak részleteit tagolva: az oszlopsor hátsó tagja tölti be a függőleges skála szerepét. Az oszlopok elé függesztett üveg-pajzsok közbülső bordái képezik a mérce-osztásokat .
Az első üvegmező pontos megrajzolásához foltjába képzelem a beleírható négyzet-hálót, (azaz két főméretének arányát állapítom meg) - a többi osztást már ehhez viszonyíthatom. A következő megoldandó részlet a közeledni látszó oszlopsor felső kontúrja. A részletről-részletről való foltépítés a gyakorlatban azt jelenti, hogy a " megelőző" méret az egység .
Nemcsak az oszlopok körvonalát keresem meg, hanem az oszlop-közöket is arányhelyesen rögzítem. A közökbe - a takarásos perspektíva szabályai szerint - folytatólagosan a háttér-vonal szakaszai kerülnek. Az eltakart részek kihagyása (korlát, kirakat, párkány stb.) a térsíkok közti távolság illúzióját kelti.
A közöket rész-osztásaikkal ábrázolom. A korlátoknál a felület-osztás, ill. anyagjelölés folt-sűrítéses módszerét alkalmazom. Az árkádok alatt eltévednék, ha nem jelölném be azonnal a pozitív és negatív formákat.
A tárgyak formáját megjelenítő körvonal és térbeli helyzetüket meghatározó környezeti vonal-háló összemetsződéseire külön gondot kell fordítani.
Az azonos magasságban levő osztások pontjaira fektetett képzeletbeli érintők az összetartás segéd-vonalait adják ki. Így sorakoznak pl. az oszlopfők és a bordák. Ezek az egy pontba összetartó vonalak éreztetik a nézővel a horizont helyzetét is.
A takarásos perspektíva alkalmazása azonnali mélységhatást eredményez, s ezáltal az előtér (oszlopok) és a háttér (üzletfal) térsíkja egymástól elkülönül.
Végre összeérnek a részletek: a rajznak ez a közbülső állomása visszaigazolja, hogy eddig rendben haladtam. (Itt: a felső födém-perem két széle találkozik).
|
|
|
|
(M)
(N)
(O)
(P)
(R)
(S) |
Az első oszlopköz véglegesítéséhez megállapítom a mező szélességét úgy, hogy a már elkészült függőleges magassághoz viszonyítom. Ez a közelebbi oszlopköznél berajzolt egyszerű geometriai formával történik. Minden felület-osztás (csempe, korlátvas, növény stb.) alkalmas részlet a foltok tagolására.
A padló-él ferde vonalként vág bele a korlátmezőbe (Később, a szélességi méretek pontosításához, leszámolom a korlátmezőket).
Az első gondos ferde-mérés az aula szemközti térfalának korlátpereménél esedékes. Nem vízszintes, hiszen a rajzoló képsíkjával a híd korlát-síkja nem párhuzamos. A korlát alapvonalhoz viszonyított helyzetét előbb a rajzlap megemelt felső peremével mérem, majd az " aránymérővel " ellenőrzöm.
A horizont érzékeltetése következik - a leghátsó híd-korlát feletti enyészpontra vízszintest illesztek. (Az ott álló alakok fejmagasságában van a rajzoló szemsíkja is.)
A függőleges egyenesek egymás alá kerülnek: a jobboldali sarokoszlop éleit folytatom lefelé. Mivel "nagy-tér" rajzolásakor a szemlélő hajlamos nézőpontját egyszerre több látványmező átkarolásával túlságosan kitágítani, vigyázni kell a függőlegesek elhajlására. (A nézőpont kiválasztásánál eldöntöttem, hogy most nem akarok harmadik iránypontot.)
Végre van mihez viszonyítani az emeletmagasságot - a felső szintről lefelé lépegetve, de a takarással is számolva - az előbbit átmérem a következőre. Ezen a rajzon a függőleges skála a közeli híd-térfal jobboldali sarokoszlop-sávja lett. Újra beigazolódott a terek egyszerűsítésének tétele (2.1.1.), amely szerint a tér-belső ábrázolásához egy nagy-kocka belsejébe képzelhetjük magunkat.
Most a felső emelet két közeli oszlopa közti - trapéznak látszó - mező keretét fejezem be: ez a vízszintes skála (" szélességi araszolás ") vége. Belelátok az iránypontba; a folyosó-szakasz képsík-vetületei, mint trapézok ill. négyzetek látszanak. Ha már egyik méretük adott, a másik hozzá viszonyítható.
|
|
|
Ha a részekből egy "emeletre-való" mező elkészült, összefogott egységként mérhetem azt a következő szint szerkesztéshez - ismétlődő elemekről lévén szó.
A középső szint oszlopát részletezve lefelé haladok, úgy, hogy azt belül a csempe-felület harmadánál, kívül pedig, ahol a vitrinfal lába belemetsz, részeire is osztom. Ez a lábazati él újra igazolja az egy iránypontos rész távlatát. Az összetartás és a takarás együttesen fokozza a mélység látszatát.
Minél jobban rálátok a belső utca vízszintes síkjainak párhuzamos éleire, annál meredekebbnek látszanak a ferdék, mert messzebbre kerülnek a szemsíkomtól. |
|
|
(T)
(U)
(V)
(Z) |
A teljes rajz-felületet a pozitív és negatív formák összessége adja ki; mintha egy üvegablak ólom-keretes mezői lennének. Ezeket bontom tovább, az aránymérés szempontjából egyszerű geometriai formákra (lásd még: 1.2.11.). Az EGF-idomok két méretükkel egyértelműen jellemezhetők.
A szemközti felület megrajzolt osztásrendjéhez képest ferdül a közeli híd korlátfogódzói. A távolodó mellvéd-sor osztásai is szöget zárnak be a hátsó fal koordináta-rendszerével. Ferde-meghatározásra megint az aránymérőt alkalmazom. Helyi sajátosság, hogy az "oszlopsornak" látszó, függőleges előtét-sor lefelé keskenyedő világító "pajzs". Formáját - vetületein keresztül - egy közeli példányánál értem meg. Ezt a módosítást "hátrafelé" egyre szűkülő méretekben visszamásolom a sor társ-elemeire is. Az elkeskenyedő pajzs-végződéseket a híd alatt fejezem be, ahol kibukkannak a takarásból.
A " folt-sűrítés " technikája szerint a közöket részleteikkel töltöm ki. Ezek pl. felület-osztások (korlátvas), anyagjelölések (kerámia-burkolat), stb. sűrűsödő vonalai lehetnek.
A léptékadó figurák laza körvonala a foltsűrítés ellenpárja. Itt a vonalhiány módszerével érzékeltetem a térsíkok közti mélységet. Az alakok mérete - de helyzete is - térbeli helyüket fejezi ki. Így pl. rálátni a szemsík alatt közlekedő figurákra - nekidőlnek a korlátnak, tehát tengelyük annak síkjával szöget zár be; lábfejük feljebb kerül, mint a födém pereme, stb |
|
|
A fekete kabát-tömegek hátterében a rács-rudaknak csak egy része rajzolódik ki. Az előtérben két vonallal ábrázolható a pálcasor kontúrja; a távolabbi közökben csak egy-egy, szakaszosan elindított vonal szerepel.
Most érkezem vissza a kiindulási ponthoz - a vonalháló összeér. A közeli hídfal térsík- kerete bezárul. Így tudom kijavítani az első ablak-osztást (F), - ellenőrizve a vezérsík teljes kerületét.
Véglegesítem az aula-térség árkádsorának födémszéli ferdéjét is (L). Ezt a ferdét újabb méréssel ellenőrzöm. Egyes pontjaival a háttér szövevényes síkidom-együttesére támaszkodik. Rendre megfigyelem a megfelelő metszés-pontokat (I). A síkidomokra bontott rész-mezők ferdéinek igazi helyzetét végső soron a "belemetsződések" adják ki. Minden a szomszédságokon múlik - nincs tárgy környezete nélkül (lásd 1.2.1.). A távlat síkvetület-béli összetevőinek határainál, a vonalhálózat összemetsződésein keresztül válik mérhetővé.
A balkéz-felőli pajzs-sor annyira sűrűnek látszik, hogy összefoglalóan elég egyetlen trapéz-foltot rajzolnom. A felső perem kontúrjának segítségével később majd részeire tagolom. A lépcsőzés töréspontjaira képzeletbeli érintőt illesztek, amelynek enyészpontja már ismert (mint J-nél). Innen kezdve a lépések megismétlődnek.
A födém-alálátást - mielőtt azt önárnyék-hatású felületosztással sötétíteném - részleteinek berajzolásával ellenőrzöm. (A lámpatestek megszámolhatók!) Egy-egy új elemnek a régiekhez való hozzárendelése a bevetítés (N) módszerével történik. Függőleges és vízszintes vetítő segédvonallal keresem meg az új pontot az alapvonal-háló koordináta-rendszerében.
A közeli pajzs osztásai úgy készülnek, hogy lent és fent megfigyelem a borda és a kész háttér találkozási pontját (I), majd a köztes mezőt arányosan tovább osztom. Ez az egyenletes beosztású függőleges skála (G) "aranyat ér", mert ennek segítségével a maradék térháló megszerkeszthető. A korlátmezők rendszere segít a javításban. A második emelet hídja felett ellátok a belső utca végfalának aljáig. A felső mező sarok-éleit levetítem a trapéz-alakúnak látszó padlószintig.
|
Mennyire "ferde" a földszint kerülete? Ezt a többi ferdéhez viszonyított szög-állás dönti el. (Mivel az iránypontot már ismerem, az összetartást szerkesztéssel is ellenőrzöm.) Az árkádsor közeiben kiszámolom az utcafal kirakat-osztásait, majd levetítem ezeket a megfelelő mezőben.
A befejező lépések során az összetartozó elemeket csoportosítom (pl. üvegfalak, feliratok, rácsok, bútorok; ha eddig nem szerepeltek volna a részlet-háló szerkesztésében).
Az üresen maradt felületeket az egyéb távlat-kifejező eszközök tagolhatják (V). A legtakarékosabb sík-meghatározó eszköz maga a (saját osztású) felület! A végső simítást az anyagjelölések adják - grafikailag így gazdagítom a rajzot. Az azonos síkban lévő, de tónusban, anyagban vagy színben eltérő foltokat további vonalháló-rétegekkel különítem el.
A tér fokozott mélyítését pl. a korlátok közé ültetett alakok (ill. térbútorok, növények, stb.) takarásos perspektívája segíti elő.
Minél közelebb kerülök a rajz aljához, annál több lesz a részlet; szaporodnak a felületosztások, s egyre inkább megjelennek az anyag-vastagságok is. Az előtér kidolgozása a térhatást növeli. |
|
|
| |
|
| |
![]()
© Minden jog fenntartva. Dr. Méhes Balázs PhD egyetemi docens
ajánlott felbontás 1024×768
|
|