Megfigyelések
¤ Felvételi Előkészítő és Példatár
¤ Képes Kockatan
¤ Mérőképsík
¤ Tükröződő Torony-trió
¤ Körgyűrűk
¤ Székrajz Szöveggel
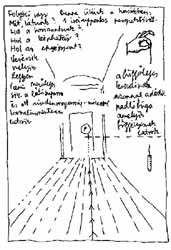
¤ Folyosórajz
¤ Fényárnyék
Szerkesztések
Külső feladatok
Kurzusok
Tanulmányok
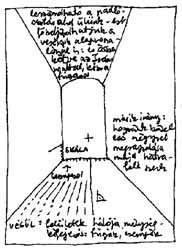
FOLYOSÓRAJZ Folyosó-szerű terek távlatrajza Egy iránypontos perspektíva, hátsó vezérsíkkal (A Műegyetem Központi épületének egyik folyosója) |
||||
Kulcs-szavak: arány, aránymérés, átlós módszer, befoglaló forma, "beülő-hasáb", egyszerű geometriai forma, főiránybeli összetevő, függőleges skála, iránypont, képhatár, képkivágás, képsík-mozaik, köztes ferde, látókúp, részlet-halmozás, szélső ferde, szemsík, szerkezeti alapvonal-háló, vezérsík. |
||||
| Tárgy- és tér-ábrázolás |
||||
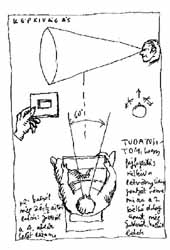
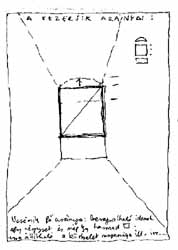
A műegyetemi rajzoktatás hagyományos tanmenetében a folyosó-rajzolás témája az első alkalom, hogy tárgyak ábrázolását követően teret rajzolunk. A tér is tárgy, csak éppen léptéket váltunk! Ha képzeletben felnagyítjuk a kockát, s helyet foglalunk benne (vagy másfelől közelítve - lekicsinyítjük magunkat, s úgy bámuljuk belsejét), elméletileg eljutunk a tárgytól a térig. |
||||
|
||||
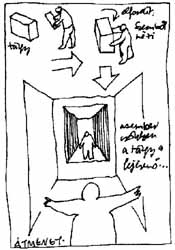
A következő vázlat egy megváltoztatott méretű négyzetes oszlop segítségével a tárgy- és térrajz közötti átmenetet szemlélteti. A tárgyat megfoghattuk, körbejárhattuk - a horizontunk általában felette volt. Ha elfordítjuk a hasábot, s szemből nézünk bele, szimmetrikus, hosszúkás, folyosó-szerű teret kapunk. Ez a hasáb szabályos kockák sorolásából épül fel. |
||||
|
||||
| Kompozíció, képkivágás |
||||
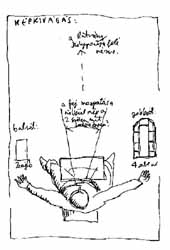
Szerkezeti vázlatunkat a képmező felosztásával kezdjük. Tárgy-rajzolásnál megtanultuk, hogy a teljes kép a főtémából és annak környezetéből tevődik össze. A környezet részeit az előtér, a háttér és a két oldalmező alkotják. Térrajznál a képmezőt a "vezérsík" és a "beülő hasáb" oldallapjainak látókúpba eső sávjai adják össze. |
||||
|
||||
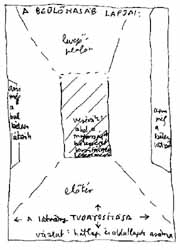
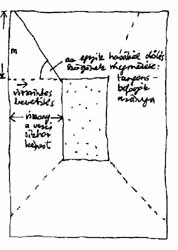
A mellékelt illusztráció a dobozbelső hátlapjának és oldallapjainak elrendezését szemlélteti. A padló ill. a plafon képsík-mozaikjainak aránya elsősorban a rajzos nézőpontjától függ. Mivel példánkban a szemsík közelebb esik a padlóhoz, mint a mennyezethez, a plafon képsíkbeli vetülete nagyobb lesz a padlóénál. |
||||
|
||||
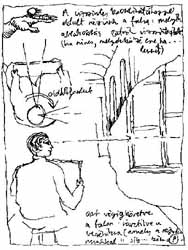
tívikus torzulásaira vonatkozó adatait ezen a képzeletbeli, átlátszó felületen gyűjtjük be és hasonlítjuk össze. "Arányméréskor" innen visszük át rajzunk síkjára megfigyeléseink (aránypárként feldolgozott) eredményét. |
||||
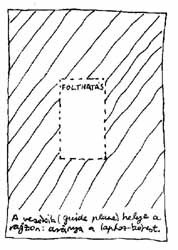
A tárgy-rajzolás szerkezetépítő fázisában a tárgyat befoglaló formába burkoltuk. Tér-rajzolásnál első vázlatunk a "dobozbelső" oldalainak kontúrhálója lesz. Kezdetnek a látvány súlypontjába eső, központi vezérsík helyét érdemes kijelölni. |
||||
|
||||
A tárgy- és térábrázolást összehasonlítva, mindkét esetben közös alkotó tevékenységnek bizonyul tehát a síkkompozíció, ami a rajz-felület kedvező arányú tagolását jelenti. A képsík-mozaikok egyensúlyát keresve, foltjaik ritmusát mérlegeljük, de a sötét ill. világos foltok váltakozására is ügyelünk. |
||||
| A vezérsík |
||||
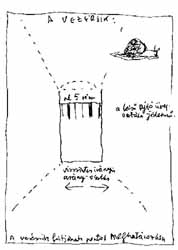
Mérő-képsíkunkkal párhuzamos felületen (itt: a szemközti üveg-ajtós válaszfal) a rajzlap széleivel párhuzamos főirányok eredeti, derékszögű hálózata perspektívában nem torzul. Ezt a felületet vezérsíknak hívjuk. A szerkezeti vázolás kezdetén az ilyen képmező megfelelő hely vízszintes és függőleges mérő-skáláink kiépítésére. |
||||
|
||||
|
||||
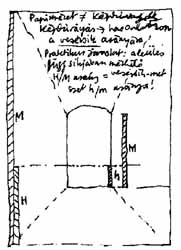
A kisebbik oldalt a nagyobbikhoz mérjük. A szemközti falat egyszerű geometriai formákra bontjuk. (A példánkban szereplő folyosó végfalánál egy egész egy harmad négyzet adódik.) A körív legfelső pontjára fektetett érintő segítségével a maradék körszeletet is szabályos téglalapba foglaljuk. |
||||
| Szélső ferdék dőlése |
||||
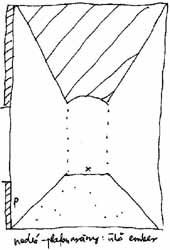
Szabályos "beülő hasábunknak" négy összetartó sarok-éle van. Padló-közelből rajzolva, a felső hasáb-élek meredekebbek, mint az alsók. Középről a mennyezet sarok-élei azonos dőlésűeknek látszanak. Fal mentén azonban a közelebbi sarok-él tűnik meredekebbnek. Határozzuk meg a sarok-élek pontos dőlését! Szerkezeti ferde dőlés-mérése a főiránybeli összetevők vizsgálatát jelenti. Egy derékszögű háromszög befogóit kell összehasonlítanunk, ahol a kérdéses ferde egyenes átfogóként szerepel. Ez az aránymérés módszere. A virtuális befogókat a korábban pontosított vezérsík főiránybeli skáláihoz viszonyítjuk. A doboz-belső összetartó |
||||
|
||||
|
||||
| Iránypont |
||||
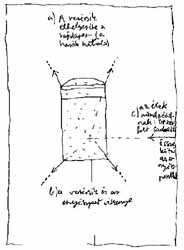
Ha a szélső ferdék meghosszabbításai (itt: a "beülő-hasáb" átellenes élei) rajzon belül metszik egymást, akkor egy iránypontos perspektívával van dolgunk. Ebben az esetben a másik iránypont jobbra-balra eltávolodik a végtelenbe, azaz a kocka-doboz képsíkunkkal párhuzamos, horizontális élei vízszintesek maradnak. A képsíkunkra merőleges síkok vízszintesei pedig határozottan egy iránypont felé futnak. Ez az összetartás jelensége. Az iránypont függőleges koordinátáját az a padló-fúga jelöli ki, amelyik éppen függőlegesnek látszik. Pillantsunk lábunk elé (hiszen rajta ülünk vagy állunk), s kísérjük szemünkkel ezt az osztást a látvány közepébe. A távoli vezérsík padló-metszékén is kiszámolható ez a koordináta. A nézőpontunkhoz tartozó iránypont vízszintes koordinátájának bejelöléséhez oldalt pillantunk, majd kikeressük a szemmagasságunkkal egyező fal- vagy ablak-osztást. Végigkövetve ezt a csíkot az oldalfalon, felvisszük a szemközti vezérsíkra. |
||||
|
||||
| Felületosztások |
||||
Végül a rövidülő térhatároló felületekre is felület-osztásokat viszünk. Példánkban a falburkoló csempékhez és a padlólapokhoz tartozó fúgákról van szó. A szerkezeti alapvonal-háló sűrűsége az iránypont közelében nő. Ez bizonyos mértékű elő-tónust is jelent - a távlati kép mélységi hatása általa is erősödik. |
||||
|
||||
| Másodlagos elemek |
||||
|
||||
ÖSSZEFOGLALÁS |
||||
Rajzlapunk síkkompozíciós felosztása során tárgy-rajznál a befoglaló forma és környezete viszonyát mérlegeljük, tér-rajznál pedig a központi vezérsík és a "beülő-hasáb" oldalainak kontúrhálóját vázoljuk fel. |
||||
Mivel a képsíkunkkal párhuzamos felületek eredeti, derékszögű alapvonal-hálózata perspektívában sem torzul, folyosó-szerű, hosszúkás terek szerkezeti felépítését célszerű a szemközti vezérsík foltjának elhelyezésével kezdeni. |
||||
| Vízszintes és függőleges koordinátái révén megkeressük az iránypontot. |
||||
A szélső ferdék dőlését arányméréssel határozzuk meg, majd kiegészítő szerkesztéssel is ellenőrizzük az összetartást. A valóság többi vízszintese (mint "köztes ferdék") a szélső ferdék által kijelölt szög-csúcs felé irányulnak. |
||||
*Jelen füzetben szereplő szöveges rajzaim 1983-ban készültek: "Kis Trakta a Folyosórajzról" címmel |
||||
© Minden jog fenntartva. Dr. Méhes Balázs PhD egyetemi docens ajánlott felbontás 1024×768 |
||||