Megfigyelések
¤ Felvételi Előkészítő és Példatár
¤ Képes Kockatan
¤ Mérőképsík
¤ Tükröződő Torony-trió
¤ Körgyűrűk
¤ Székrajz Szöveggel
¤ Folyosórajz
¤ Fényárnyék
Szerkesztések
Külső feladatok
Kurzusok
Tanulmányok
MÉRŐKÉPSÍK A Távlati Kép Szerkezetének Ferde Vonalairól A "MÉRŐKÉPSÍK " OKTATÁSI SEGÉDESZKÖZ LEÍRÁSA (Egy régi találmány újszerű alkalmazása) |
||||||||
Kulcs-szavak: aránymérés, befoglaló forma, "ceruzás"-mérés, dőlésmérték, felezősík, főirányok, alapvonal-háló (AVH), mérőképsík, mértékadó ferdék, Y-csomópont, vezérsík. |
||||||||
Kísérleteim a "Mérőképsíkkal" a BME Rajzi Tanszékén. Elsőéves mérnökhallgatók kockológiája (K.ép.III.em.IV-es terem, 2000. őszi félév) |
||||||||
| Bevezetés |
||||||||
A mérőképsík bemutatása az oktatás kezdetén, a vonalperspektíva elméletének bevezetésekor időszerű, amikor a távlattan alap-jelenségeinek ismertetésével foglalkozunk (centrális projekció, összetartás, rövidülés, iránypont, szemsík). Az építészeti szabadkézi rajz szerkezeti felépítése során a látvány "ferdéinek" pontos ábrázolása döntő jelentőségű. A hallgatók előtt általában homályos a "nyújtott karral való ceruzás mérés" eredete. Bár a gyakorlatban sűrűn alkalmazzák a (főleg egymástól ellesett) szokványos mozdulat-sort, gyakran hibás a kéz- ill. kar-tartás. Az egyszerű vonalhálóra redukált távlati kép mélységi hatásáért egyrészt a ferdének látszó vonalak (másrészt pedig a vonalak sűrűsödése ill. a vonalak hiánya) felelősek. Emeljük ki a szerkezeti háló ferde vonalainak jelentőségét! A ferdéket a képsík (illetve a rajzlap) széleihez képest érezzük ferdének. A téglalap-alakú rajzlap szélei képviselik a biztonságot nyújtó főirányokat. Főirányaink a rajzon: a vízszintes és a függőleges. A ferde vonalakat főirány-beli összetevőikre bontva elemezzük. A szerkezeti váz ferdéinek gondos megfigyelése (azaz dőlés-mértékük nézőpontunknak megfelelő megállapítása) nagyon fontos az alapvonal-háló felvázolásának szakaszában. |
||||||||
|
||||||||
|
||||||||
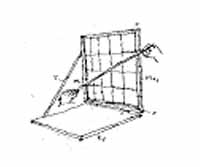
A kísérletben szereplő mérőképsík keretét vékony húrokkal (négyszer öt arányban) négyzet-mezőkre osztottam. A keretet csuklós-pántokkal egy A/2-es rajztábla felső éléhez illesztettem. A rámát néhány "aránymérő"-gyakorlat után egyszerűen lekapcsolom a rajztábláról. |
||||||||
| A szerkezet méretei |
||||||||
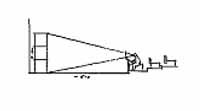
A mintapéldány egy A/2-es méretű, szabványos rajztábla felső pereméhez csuklópántokkal csatolt, hálós keretet mutat be. A könnyű, levehető fa-keret lehajtott állapotban éppen rásimul a rajztáblára, hogy beleférjen a rajztábla-tartó mappába. Mérnök-hallgatóimmal elvégzett kísérleteim ezt a választott méretet igazolták vissza. Ha kisebb lenne a rajztábla és a rászerelt "mérőképsík" (pl. A/3-mas), akkor a ráma csak a látvány közeli részletét foglalná keretbe. |
||||||||
|
||||||||
| A "Mérőképsík" használata: |
||||||||
A mellékelt feladat-sor szerint vizsgáljuk sorra a szerkezeti alapvonal-háló jellegzetes csomópontjainak leegyszerűsített eseteit! Határozzuk meg rendre a mértékadó ferdék nézőpontunknak megfelelő dőlés-mértékét! A gyakorlatnak az a célja, hogy részletezzük a képsík-beli ferdék rajz-síkra való átültetésének mentális folyamatát. |
||||||||
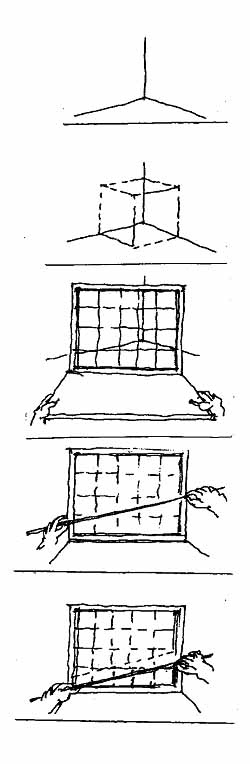
• A látvány az ábra szerinti képsík-kereten (Mks) keresztül jelenik meg a szemem előtt. • A csuklós kitámasztó rúd (T) segítségével a megfigyelési nézősugárra merőleges helyzetűre állítom a "mérőképsíkot". (Hálójának függőlegesei közvetlenül párhuzamba hozhatók a látvány függőlegeseivel.) • A kiválasztott ferdét - a mérőpálcával a hálós képsíkon mozogva - letakarom, s egyben a keret széléig meghosszabbítom. A rövid ferde szakaszból egy csapásra nagyobb (vagyis jobban mérhető) ferde vonal lesz. • Az így kiegészített ferdét egy derékszögű háromszög átfogójának tekintem. • A ferdének főirány-beli vetületei képezik a derékszögű háromszög befogóit. • A vizsgált ferde vonal dőlés-mértékét a keret-menti befogók összevetésével állapítom meg. A "mérőképsík" hálós oldal-beosztása révén a dőlés arányát számokkal is kifejezhetem. Értékét addig kell megjegyeznem, amíg az aránypár hiányzó tagját fejben kiszámolom. • Ezt az arányt aránypár részeként viszem át a rajz síkjára. (Adottnak tekintem a befoglaló forma kezdő méretét, mint egyik befogót; ehhez társul most a leolvasott dőlés-mérték törtje - a keresett mennyiség a rajzra átviendő másik befogó lesz.) |
||||||||
A bemutató elején (vagy ismételt értetlenség feloldására) a leolvasási értékek időleges fejben tartására használhatom a perem-menti számoló-rudak (nyom-rögzítő) gyűrűit is. |
||||||||
|
||||||||
|
||||||||
| Forgatókönyv a "Mérőképsík" oktatási segédeszköz bemutatójához |
||||||||
|
A rajzbakra helyezett "mérőképsík" segítségével a vonalperspektíva alapjelenségeit kézzelfogható módon tudom elmagyarázni. A táblán a mellékelt ábrasor jeleníthető meg. Célszerű az eszközt félprofilból bemutatni. A demonstrációs segédeszköz a gyakorlatok megkezdése előtt néhány elméleti fogalom körülírására is alkalmasnak bizonyul. Így pl. az összeállítás segítségével magától értetődően szemléltethetem, miért szükséges a rajz-bak hossztengelyével - vagyis a felező-sík talpvonalával - megcélozni a téma súlypontját? A szerkezet síkjainak elrendezése azt illusztrálja, miért kell a pontos távlati hatás elérése érdekében a rajzolási nézősugárnak merőlegesnek lennie a rajzolás síkjára? (A rajzoló felező-síkja egyaránt tartalmazza a rajzolási és a megfigyelési nézősugarat.) |
||||||||
| Kísérő témák a demonstrációs eszközhöz: |
||||||||
| • "Rácson át rácsodálkozni a világra" - Dürer szellemének felidézése • A perspektíva (mint centrális vetítés) magyarázata • A centrális vetítés elemei (szem, nézősugár, képsík) • A "Mérőképsík" kiválasztása • Összetartás-rövidülés (kockaháló vetületein keresztül magyarázva) • A ferde vonal képsíkbeli keletkezése • Az arány szemléltetése és számszerűsítése • Dőlés-mérés a főiránybeli vetületek összevetésével • A "mérőképsík" behelyettesítése (a "ceruzás mérés" bevezetése) |
||||||||
A tanítvány kikeresheti a legkedvezőbb képkivágást. Használata közben begyakorolja a pontos irányba való leülést és a helyes rajztábla-tartást is. A háló függőlegeseit a látványéihoz igazítva, kitapasztalja a mérőképsík helyét. A keretes "Mérőképsík" bevezeti az összecsukható "Aránymérő" kipróbálását. |
||||||||
| A "Mérőképsík" és az "Aránymérő" összevetése: |
||||||||
A két eszköz hasonló elven működik. Használatuk egymásra épül. Az egyik konkrét, a másik elvontabb. Az "Aránymérő" pálcája egy olyan virtuális képsíkot súrol, amelynek kereteit csak lelki szemeink látják. A következő lépés a magunk elé nyújtott karral való "ceruzás mérés" gyakorlása lesz Végül pedig szabad szemmértékkel dolgozunk. A keret pontosan kijelöli azt a választott képsíkot, amelyen a szerkezeti alapvonal-háló perspektívikus torzulásának adatait észleljük. Az "aránymérő" egy szinttel elvontabb; használata feltételezi a mérőképsík helyének ismeretét. A keret levehető, a mérő zsebre-dugható, hogy később a szabad rajzolást később ne akadályozzák. Mindkét szerkezetet csupán az oktatás kezdeti időszakában, az elméleti bemutató demonstrációs eszközeként javaslom használni. Véleményem szerint, megfelelő pillanatban és jól előkészített környezetben alkalmazva, ezek a "kézzelfogható" szerkezetek a rajz-oktatást hatékonyan kiegészíthetik. Bármelyik segédeszközt alkalmazzuk is, ne tévesszük szem elől eredeti szándékunkat: oktatási célunk végső soron a megbízható szemmérték kifejlesztése legyen! Oktatási módszertani segédeszközként a hallgatók kérdéseit segít megválaszolni. Ne akadályozza viszont a szabad képkivágást és az önálló rajzolást! |
||||||||
| Hivatkozás korábbi módszerekre |
||||||||
Emlékeztetőül álljon itt a közismert Dürer - metszet! Érdemes visszatekinteni, hiszen számítógépes korszakunk nagy elődök felfedezéseire épül. |
||||||||
|
||||||||
ÖSSZEFOGLALÁS |
||||||||
A "Mérőképsík" kézzelfoghatóan demonstrálja azt a kitüntetett képsíkot, amelyről a szabadkézi rajz szerkezeti felépítésének folyamán a látvány perspektivikus torzulásának adatait saját rajzunkra átvisszük. Az adatok átvitele nem gépies másolással, hanem aránypárok elvén alapuló, összehasonlító elemzéssel történik. Az első vázlat befoglaló formája tartalmazza az aránypárnak azt az elemét, amelyhez a megfigyelt dőlés-mérték tört-számát rendeljük. A későbbiekben ezt a képsíkot a rajzoló előtt kb. Karnyújtásnyi távolságban képzeljük el. A "mérőképsíkra" a "ceruzás méréssel" emlékezünk. |
||||||||
Tapasztalatom szerint a hálós keret kipróbálásával tanítványaim gyorsan megértik a virtuális képsík jelentőségét. Néhány egyszerű példát ajánlok a szerkezeti alapvonal-háló jellegzetes csomópontjainak begyakorlására. |
||||||||
Melléklet: Húsz gyakorlati példa a "Mérőképsík " használatára |
||||||||
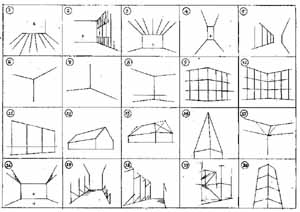
A bemutatott gyakorlati példák száma egyben utalás a prototípus 5x4=20 mezőjére. Járjuk be együtt jelképesen a "mérőképsíkot"! Válasszuk ki együtt a mértékadó ferdéket! A mérőgyakorlat témája a legszélső ferdék dőlésének meghatározása. |
||||||||
A térbeli alapvonal-háló (AVH) elsőrendű részei: a kockaháló élei |
||||||||
| Egy iránypontos esetek: |
||||||||
| 1. Padló-rácsozat tanulmányozása (a vízszintes sík párhuzamos osztásainak összetartása) 2. Ablak-sor (a függőleges sík osztás-hálója) 3. Mennyezet-gerendák (álmennyezeti osztások, lámpasorok, alálátás vízszintes síkra) 4. Folyosó-szerű, hosszúkás tér 5. Utcafal (egyenes utca homlokzat-sorának ereszvonalai és lábazatai |
||||||||
| Két iránypontos esetek: |
||||||||
| 6. Y-csomópont, szabályos belső tér felső sarka (alálátás) 7. Y-csomópont, szabályos belső tér alsó sarka (rálátás) 8. Tágas belső tér sarka, alacsony horizonttal 9. Pozitív épület-sarok 10. Negatív épületsarok (pl. belső udvar) 11. Homlokzat vagy utcafal, félprofilból (a nagyon távoli iránypont esete) |
||||||||
Az AVH másod- és harmadrendű elemei: lap- és tér-átlók (tető, lejtő, lépcső) |
||||||||
| 12. Oromfal (vagy: tympanon) 13. Kontyolt nyeregtető éle (Az általános ferde vonal mint tér-átló első megjelenése) 14. Toronysisak (gúla, pozitív hajlat) 15. Nyeregtetők összemetsződése (vápa, negatív hajlat) 16. Ferde síkú mennyezet alulnézetben (alálátás ferde síkra, 1 IP) 17. Lejtő,aluról nézve (ferde sík ráillesztése az alapvonal-hálóra) 18. Lejtő, felülről nézve (az AVH lap-átlói) 19. Összetett ferdék előfordulása: lépcsőkarok és korlátok példája |
||||||||
| A harmadik iránypont megjelenése: |
||||||||
| 20. Torony-alálátás |
||||||||
| |
||||||||
| Az AVH-minták kiválasztásának szempontjairól |
||||||||
Az egyszerű esetektől az összetettek felé haladunk. Az ábrázolandó síkok helyzete szerint válogatunk. Hagyományos tanmenetünk szerint a belső terek rajzolása után jutunk el a külső helyszínekig. Az elvont formák megjelenítése után következhetnek csak igazi épülettömegek. Az iránypontok száma szerint is sorba rendezhetők a minták. Példáinkat a főtéma AVH-jának a képsíkkal bezárt szöge szerint is csoportosíthatjuk: vajon meredekebb avagy laposabb szögből nézzük-e a látványt? (A lapos variációnál előforduló "majdnem-vízszintesek" rajzolása a nehezebb feladat.) Mindegyik alapeset a szabályos kockahálóra vezethető vissza. Ezt szerkezeti alapvonal-hálónak (AVH) nevezzük Az AVH rendszere jól áttekinthető első-, másod és harmadrendű főirányokból tevődik össze. Az alapvonal-háló elsődleges elemei a kocka-élek. Ezután következnek a másodrendű lapátlók, majd a harmadrendű térátlók. Gyakorlatilag mindenütt élek, lapátlók s térátlók egymásra épülő hálózatáról van szó. A főirányok ismertetése után az alap-síkokba fektetett egyenesek következnek. Leírásukhoz a kétirányú lapátlók szükségesek. Így jutunk el az "általános ferdékig", amelyeket a tér-átlók képviselnek. Ezek leírásához már háromféle vetületet veszünk igénybe. A kockákat hasábokká alakítva, három lépésben a látvány bármelyik ferdéjéig eljuthatunk. A diákok figyelmét leköti, ha film-szerűen, pontról-pontra előttük bontakoztatjuk ki a távlati hatást. Eközben bepillantunk az építészeti szabadkézi rajz egy távolabbi fejezetébe is. A távlati kép vetületekből történő helyreállításákor ugyanis egy megfelelően kiválasztott, első kockából vezetjük le a szerkesztést. Az egy iránypontos perspektíva különleges esetével kezdem a foglalkozást. (Ebben a speciális helyzetben a képsíkkal párhuzamos az alapvonal-háló kocka-rácsa.) Ilyenkor könnyebb a horizont mozgatása során az alapvonalháló rácsozatán bekövetkező perspektívikus torzulásokat követni. A két iránypontos esetek is szétbonthatóak, különvéve az "alsó" és a "felső" Y-csomópontokat. (Az egyik az alálátás, a másik a rálátás esete.) A sík terep után következik a lejtő, amely bevezeti a lépcső tárgyalását. A nehezebb témákra "oda és vissza" is nézzünk rá! A lejtőre először alulról, azután pedig felülről tekintünk, hogy a lábazati háromszögek jelentőségét kihangsúlyozhassuk. A síkok helyzetét felületosztással jelöljük meg. Az alapformákból egy füst alatt néhány gyakran előforduló tetőforma is levezethető. Célszerűnek tartom azt, hogy minél előbb ismertessük meg hallgatóinkkal az építészeti szabadkézi rajzban lépten-nyomon használatos szerkesztési eljárásokat is! Akár a legelső sémánál is tanítható már pl. az átlós szerkesztés "szakasz-szaporító" módszere. A gúla-formájú toronysisak rajzolásakor mutassuk be, hogyan figyelhető meg az általános ferde élnek a függőlegestől való eltérése? Szerkesztéssel is ellenőrizzük az eredményt! (Az alap-négyzeten - átlók segítségével - kikeressük a középpontot, s erre állítjuk fel a gúla magasságát.) |
||||||||
|
||||||||
A minták felsorolását számtalan variációval folytathatjuk. Így pl. az egyik leggyakoribb változat épülettömegek sarok-"levágása" illetve további ferde síkok AVH-ra-való ültetése. Példáinkat érdemes közvetlen környezetünkből meríteni, hogy a hallgatókban tüstént emlék-kép keletkezzen. Eközben törekedjünk a sémák mielőbbi építészeti felhasználhatóságra is! Mivel Egyetemünkön a szabadkézi rajzoktatás kezdeti szakasza időben legközelebb a lakóépület-tervezési tantárgyhoz kapcsolódik, kézenfekvőnek tűnik egyszerű lakóépületeket felidézni. Lehetőleg olyan példákat mutassunk be, amelyeknek valóság-beli megfelelője az oktatás minden részvevője számára elérhető közelségben van. A szögletes testek, terek egyeneseinek tárgyalása után a következő fejezet legyen az előbbiekből származtatandó "íves világ"! Ez az elsőre épül: az út elfordul, a vonal elgörbül, a sík behorpad, vagy kidomborodik. A réteg- és esésvonalak segítségével a síkok hullámzani kezdenek. Változatos tető- és tömegformákat, ill. belső tereket mutassunk be! Hogyan rajzolható pl. a dongaboltozat, a csigalépcső, a körgyűrű, a hártya, a vitorla, a hagymakupola, a sátor? A felületek görbületeit felületosztások hálózatával érzékeltetjük. Kézenfekvő az előző rész "szögletes" ábráit megfelelő íves formákkal egyenként behelyettesíteni. (A táblán az egyeneseket meggörbítem, a síkokat íves felületűre hajlítgatom, a térhatároló elemeket módszeresen átformálom.) Aki képes a természet utáni látványt pontosan megörökíteni, az saját építészeti ötleteit is jobban közli majd másokkal! |
||||||||
© Minden jog fenntartva. Dr. Méhes Balázs PhD egyetemi docens ajánlott felbontás 1024×768 |
||||||||