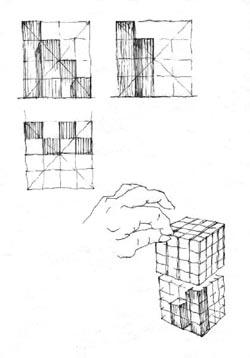
Megfigyelések
Szerkesztések
¤ Perspektíva Helyreállítása Vetületekből
¤ Első Kocka - Szélső Kocka
¤ Kockarács
¤ Fókuszban a Térsarok
¤ Térsarok Kockatoronnyal
¤ Vetett Árnyék Szabadkézzel
¤ Ablakok
¤ Épület és Növény
Külső feladatok
Kurzusok
Tanulmányok
ELSŐ KOCKA - SZÉLSŐ KOCKA |
||||||
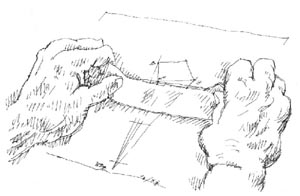
Vetületek hasznosítása a szerkezeti alapvonalháló kezdő kockájának szabadkézi felszerkesztésében (A "papírcsík-módszer") |
||||||
Kulcs-szavak: aránypár, átlós módszer, befoglaló forma, centrális projekció, előválasztott oldallap-arány, felezősík, iránypont, köztes ferde, nézőpont, nézősugár, szélső ferde, tárgy-képsík, szerkezeti alapvonal-háló, sziluett-hatszög, vetület, vezérsugár. |
||||||
| Szerkezeti rács és szélső ferde |
||||||
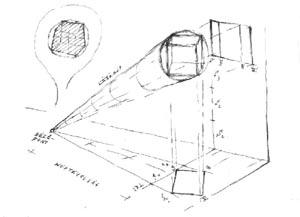
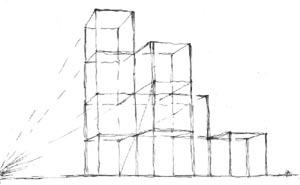
A címbeli kocka a Perspektíva Helyreállítása Vetületekből (PHV) típusú szabadkézi rajzfeladatok főszereplője. Amennyiben sikerül a távlati kép szerkezeti alapvonal-hálójának legelső kockáját helyesen megjelenítenünk - fejből, akkor a többi rács-pontot átlós módszerrel már szerkeszthetjük. Az átlós módszer a kocka-háló sarokpontjainak átellenes oldalfelezőn való tükrözését jelenti. A vízszintes síkokhoz tartozó, párhuzamos egyenesek összetartásukkal kijelölik saját iránypontjuk helyét a horizonton. Az iránypontok egyike-másika gyakran kívül esik rajzlapunk felületén. Felderítésük céljából mielőbb állapítsuk meg a legmeredekebb oldal-élek látszólagos dőlését! A távlati kép szerkezeti felépítése folyamán a valóság többi vízszintes elemét (pl. épületrajznál a födémeket) mint köztes ferdéket a szélső ferde és a horizont közé szorítjuk. Ezek szög-szárakhoz hasonlóan a távoli iránypont - szög-csúcsként elképzelt - valószínű helyzetére utalnak. Miután a konstruktív háló szélső ferdéit pontosan meghatároztuk, a köztes ferdék összetartó vonal-nyalábjaihoz szakaszos interpolálással jutunk majd el. A fentiekből következik, hogy a szabadkézi vetület-helyreállítások során az első kocka minősége sorsdöntő. Tanulmányom a választott nézőponthoz tartozó kezdő kocka felvázolásához kíván kézzelfogható segítséget nyújtani. |
||||||
|
||||||
|
||||||
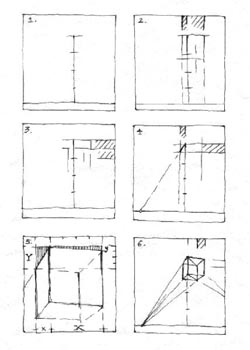
modulhálóját a választott irányból nézhessük! Ezek szerint a lap aljára kerül a nézőpont, a vezérsugár merőleges a tárgy-képsíkra. (Képsíkunk a leképezendő kocka-torony közeli éléig tolva, nevezhető tárgy- képsíknak.) Most állítsuk össze el az úgy nevezett "felezősík" (különleges oldalnézetünk) rajzát! |
||||||
Az alálátás-viszonyokat erről a "felezősíkról" olvashatjuk le. (A felezősík nevével korábban a "Képes Kockatanban" találkoztunk először, amikor a rajzoló rajzbakjának hossztengelyével megcélozta a téma súlypontját. A felezősík magában foglalja a rajzoló- és a megfigyelő-nézősugarat is. A felezősík a látvány irányába tekintő szemlélőt felülről nézve képletesen "elfelezi".) A felezősík itt egy sajátos oldalnézet, amelyet vezérsugár mentén, az alaprajzra és a tárgy-képsíkra egyaránt merőlegesen állítunk fel. Jelen példában ezen a speciális oldalnézeten tornyunknak mind a négy függőleges éle külön látszik. Ennyi útravalóval felszerelkezve már nem egészen üres kézzel kezdhetjük perspektívánk választott nézőpontból eltervezett szerkezeti felépítéséhez. Eddig úgy tanultuk, hogy az első kockát "hasra-ütéssel, fejből" kell előállítanunk. Eljárásom némi konkrét támogatást kínál ehhez a kényes művelethez. Asztalunkon tehát magunk elé terítjük a nézési irányba forgatott alaprajzot. A kapcsolódó homlokzatok lapjait is tegyük ki a megfelelő oldalakhoz! Az alálátások leolvasása érdekében egy különleges, közbülső oldalnézetre is szert tettünk az előkészítés során. |
||||||
4. ábra: A befoglaló sziluett-hatszög főméretei a választott kockához viszonyítva - |
||||||
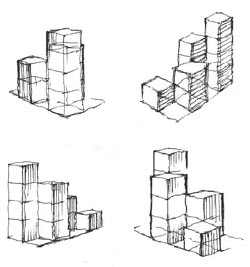
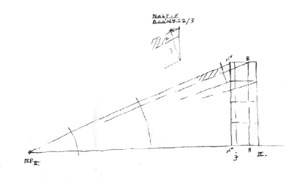
A nézőpontból ilyennek látszik a szélső kocka sziluett-hatszöge. Befoglaló foltjának össz-magassága a közeli függőleges élből és az alsó lap látszólagos magasságából tevődik össze (M = S + a), össz-szélessége a keskenyebb és a szélesebb oldallap-metszék összege (Sz = xbal + xjobb). Amíg a képtávolság kb. két-és-félszerese a nagyobbik tárgy-méretnek, addig a képsík dőlése nem jelentős, azaz a függőlegesek még nem torzulnak. Ha közelebbre helyeznénk át nézőpontunkat, megjelenne a harmadik iránypont is. |
||||||
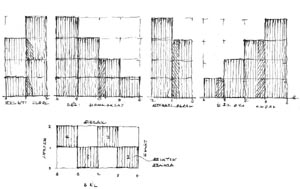
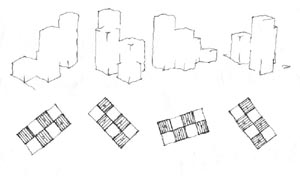
5. ábra: Sziluettek és nézési irányba forgatott alaprajzok. A vonatkozó nézőpontokat rendre a lap aljára képzeljük. |
||||||
|
||||||
|
||||||
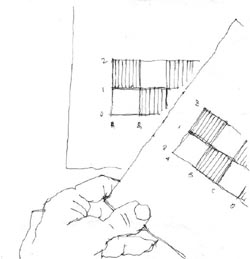
oldal-metszéket. (A negyedik függőleges él bejelölését készülő perspektívánkon későbbre is halaszthatjuk.) A függőlegesek között mért vízszintes távolságok arányrendjét(xbal / xjobb) egy papírcsík segítségével vihetjük át szerkezeti vázlatunkra. Fontos megjegyezni, hogy a vetületekről nem az "abszolút" méreteket másoljuk közvetlenül, hanem a mért adatok kocka-élhez, mint egységhez (Svetület ) viszonyított arányát! Nyilvánvaló, hogy a távlati kép kiinduló kocka-éle (Sperspektíva) viszont a rajzolás kezdetén megválasztott, eredeti befoglaló formától függ, amelyet - többek között - a rendelkezésünkre álló papír felülete, illetve a készítendő ábra mérete sugall. |
||||||
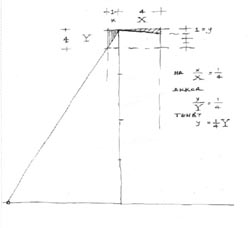
| 2 - Alálátás viszonya | ||||||
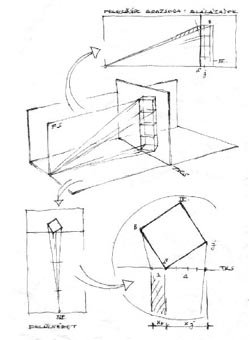
| Egy újabb papírcsík segítségével a felezősíkról átvehető a "nagy Y" sávja, azaz a fedlap alálátása. (S / B arány). | ||||||
|
||||||
| 3 - Szélső ferdék | ||||||
A legfelső pontból indítható a fedlap legmeredekebb éle (SmaxB). A szélső ferde meghosszabbítása padló-horizontunkon kimetszi a baloldali iránypontot (Ip bal). Ezután következhet a másik iránypont távoli helyének megbecsülése. |
||||||
|
||||||
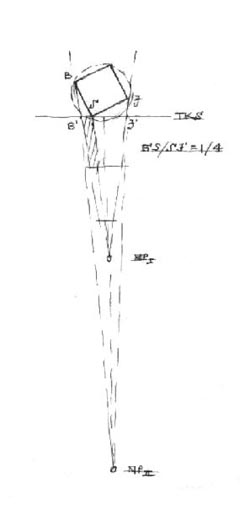
4 - Összetartások ellenőrzése Újra elővéve az alaprajzról átvett x-metszékek papírcsíkját, vázlatunkon tüntessük fel a hátsó (IV.) él helyét is! A baloldali iránypont révén az SB-peremmel párhuzamos kocka-élek összetartása sorra megvalósul. Az összetartások ellenőrzésére jól használható az átlók iránypontja. (Ip átló közelebb lévén, sokkal jobban kezelhető, mint a rajzlapon túli, csak sejthető, Ip jobb). A szerkezeti rács kiterjesztése előtt érdemes még egyszer gondosan, hunyorítva szemrevételezni elsőszülöttünket. Itt az ideje annak, hogy véglegesítsük első kockánkat! Vonatkoztassunk el minden szerkesztéstől és spekulációtól! Kizárólag saját, természet-utáni rajzolás során szerzett tapasztalatainkra támaszkodjunk ebben a fázisban! Józan szemmértékkel vizsgáljuk meg minden irányból a rajzot (forgassuk fejjel lefelé is), hogy feltétlenül hihetőnek tűnjön modulhálónk sokat emlegetett kulcs-szereplője! |
||||||
|
||||||
| A "papírcsík-módszer" | ||||||
|
||||||
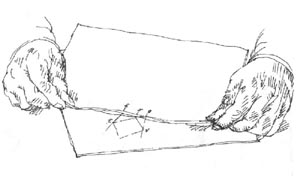
12. ábra: A papírcsík-módszer - |
||||||
Munka közben feljegyeztem, hányszor került sor adat-átvitelre: • Első csík - felezősík létesítése (a nézési irányba forgatott alaprajzról a függőleges élek közti távolságok másolása); • Második csík - a sziluett-hatszög befoglaló foltjának főméretei; • Harmadik csík -- az oldallap-metszékek aránya (xbal, xjobb, majd a hátsó, negyedik él helye); • Negyedik csík - a fedlap alálátása (nagy Y sávja, S-hez képest). Döntések és következmények Tekintsünk most vissza, s számoljuk össze a "perspektíva helyreállítása vetületekből" típusú feladatok kötöttségeit! Melyek voltak példánk szabadon választott adatai, s ezek milyen következményekkel jártak? Mi választottuk ki (a befoglaló forma felvázolása közben): • a kocka függőleges élének méretét (S); • a szemsíkot (H) - a téma magassági skálájához képest; • a nézőpont (NP) helyét - az alaprajzon tűztük ki, ezáltal rögzítve az oldallap-sávok arányát (xbal / xjobb), továbbá • a képtávolságot (KT), amelyet a felező síkon (oldalnézeti vetületen) jelöltük be, eldöntve ezzel az alálátásokat (nagy Y, kis y) Mi döntjük el, honnan nézzük, s mekkora képet akarunk (NP, KT, H, S)! Ebben az adat-sorban benne rejlik az első iránypont helye. A második iránypont pozíciója az előbbiek következménye lesz. Nem tűzhetünk ki büntetlenül túl sok adatot egyszerre! Sok zavart okozhat pl. mindkét iránypont és kockaméret ((Ip bal , Ip jobb , S) egyidejű felvétele. Ekkor ugyanis vagy nagyon kicsi ábrát kapunk, vagy reménytelenül torz eredményhez jutunk. |
||||||
|
||||||
ÖSSZEFOGLALÁS |
||||||
A "perspektíva helyreállítása vetületekből" típusú feladatok legérzékenyebb része az első kocka választott nézőpontból történő, szabadkezes felvázolása. Az első kockára a szerkezeti alapvonal-háló létrehozása miatt van szükség. Első kockánk olyan szélső kocka legyen, amelynek meredeken összetartó élei a (gyakran a rajzon túli) iránypont helyére utalnak. A kocka-rács átlós módszerrel tovább bővíthető. Az első kocka fejből történő felvázolását megkönnyíti a vonatkozó vetületekről leolvasható torzulások aránya. A függőleges élek közötti távolságokat a nézési irányba forgatott felülnézetről olvashatjuk le. A felezősíkról a vízszintes lapok látszólagos deformációját vehetjük át. Amikor perspektív vázlatunkon a vizsgált kocka-élhez tartozó kétféle vetületi sávot fedésbe hozzuk, kirajzolódik az iránypont felé mutató szélső ferde iránya. Nézőpontunk kijelölésével az oldallapok arányát szabadon dönthetjük el. Képtávolságunk megválasztásával az alálátás mértéke tűzhető ki. A legmeredekebb él megbecsüléséhez ezt a két döntést hasznosítjuk. |
||||||
|
||||||
© Minden jog fenntartva. Dr. Méhes Balázs PhD egyetemi docens ajánlott felbontás 1024×768 |
||||||