Megfigyelések


   Szerkesztések

  ¤ Perspektíva Helyreállítása Vetületekből
  ¤ Első Kocka - Szélső Kocka
  ¤ Kockarács
  ¤ Fókuszban a Térsarok
  ¤ Térsarok Kockatoronnyal
  ¤ Vetett Árnyék Szabadkézzel
  ¤ Ablakok
  ¤ Épület és Növény


   Külső feladatok


   Kurzusok


   Tanulmányok
 


VETETT ÁRNYÉK SZABADKÉZZEL*

  
 
Kulcs-szavak: árnyék-fogó felület, árnyékvető él, árnyékvető pont, "fény-doboz", fény-sík, fénysugár, kívánt árnyék-pont, lapátló, térátló, vetület.


     Bevezetés

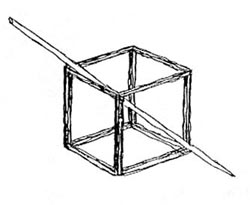
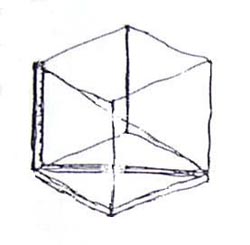
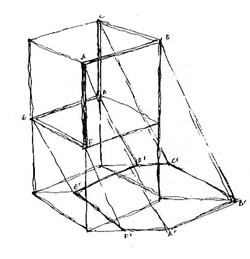
     A "fénydoboz" fogalmát a fénysugár vetületekben való értelmezése kedvéért vezetjük be. Kezdetben a fénysugarat egy kiskocka térátlója képviseli. Kiindulásul tételezzük fel, hogy ez a fénysugár éppen egybeesik ezzel a térátlójával!


1. ábra: Az alaphelyzet modellje - A fénysugarat egy kiskocka térátlója képviseli.


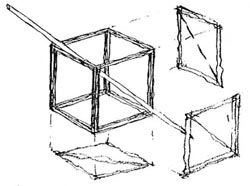
2. ábra: Alaphelyzet, kiegészítve vetületekkel - a térátló-fénysugár a kocka lapjain lapátlókként jelenik meg.


     Térátlóként választott fénysugarunk a befoglaló fénydoboz oldalsó lapjain mint egy-egy lapátló jelenik meg. A fény-sík és az árnyék-fogó felület metszésvonalát (vagyis az árnyékot) könnyebb először a vetületekben megtalálni.
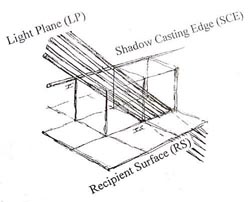
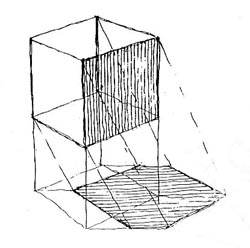
     A fénysíkot a vizsgált árnyékvető élre illesztett fénysugár-egyenesek sorozatából származtatjuk, amelyek mind párhuzamosak a fő fénysugárral.

3. ábra: A fény-sík eredete.

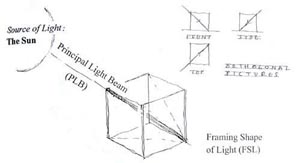
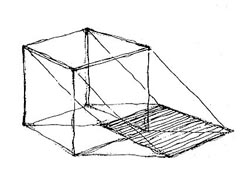
     Kezdetben tehát azt feltételezzük, hogy a fő fénysugár helyzete pontosan egybeesik a kiskocka egyik térátlójával. A felső P sarok padlóra vetett árnyékát úgy kapjuk meg, hogy ráillesztjük a fő fénysugarat (vagyis a térátlót). Ekkor az pontosan a kocka átellenes alsó sarkára fog mutatni. A felső sarok vetett árnyéka az átellenes alsó sarok lesz.


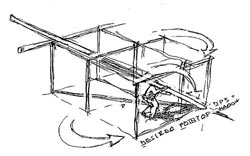
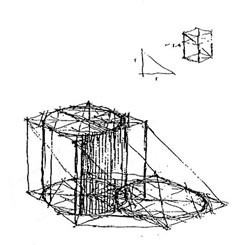
4. ábra: Fényforrás, fő fénysugár és befoglaló fény-doboz perspektivikus modellben és vetületekben.


     Szabadkézi módszerünknek az a lényege, hogy a szerkesztés kezdetén, látványtervünkön belül, a legelső választott pont vetett árnyékát a legkedvezőbb fényirány megválasztásával, mi magunk határozhatjuk meg. Gyakorlatilag rajzunk egy fontos pontjához tartozó árnyékpontot szabadon tűzünk ki. Ez lesz a "kívánt vetett árnyék pontja". Általában az előre elképzelt végeredmény, vagyis a végső kép szerkesztett árnyékokkal kiegészített kompozíciója, az elvárt hatás befolyásolja ezt a döntésünket.



5. ábra: Az árnyék kívánt pontja - visszafelé szerkesztünk,
amikor módosítjuk a térátló helyzetét.


     A kívánt árnyékpontot összekötve eredeti árnyékvető pontjával perspektívánkon véglegesítjük azt a fényirányt, amellyel mostantól fogva dolgozunk. Így alakul ki a befoglaló fénydoboz módosított formája. Az eredeti kockából valamilyen hasáb lett. Ezután meghatározzuk mindhárom vetületen módosított fénydobozunk fő méreteit. Szerkesztés közben a fénysugár vetületi képeit követjük figyelmesen.
     A következőkben a szerkezeti rácson belül leggyakrabban előforduló eseteket foglaljuk össze. .


6 - 9. ábra: Leggyakoribb vetett árnyék-helyzetek. Zárójelben az ok és az okozat van feltüntetve (V = vertikális, H = horizontális helyzet).



6. ábra: Függőleges egyenes árnyéka vízszintes
síkon (V/H)

8. ábra: Vízszintes egyenes árnyéka vízszintes
síkon (H/H)



7. ábra: Függőleges egyenes árnyéka függőleges síkon (V/V)

9. ábra: Vízszintes egyenes árnyéka függőleges
síkon (H/V)



PÉLDÁK


10. ábra: Lebegő váz-kocka vetett árnyéka (a lebegés magassága egy kockányi) A váz-szerkezet rúdjai két kockát képviselnek.


     Az árnyékvető élek meghatározásának folyamata esetünkben azt jelenti, hogy a világos és sötét oldalakat értelmesen elhatároljuk egymástól. Tömör tárgyak árnyékvető élei folyamatos vonalat alkotnak, melyek végül zárt vetett árnyék-foltot eredményeznek. Árnyék-szerkesztés közben is ügyeljünk a párhuzamos egyenesek perspektívikus összetartására!


11. ábra: Teli lapos lebegő kocka vetett árnyéka.


12. ábra: Lebegő négyzet vetett árnyéka (lebegési magasság éppen kockányi).


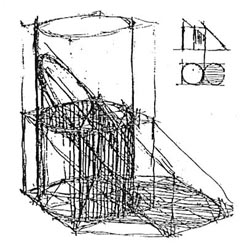
13. ábra: Befoglaló kockába írt henger vetett árnyéka.


A szerkesztés lépései:

     •     Fedlap árnyéka
     •     Kör-szerkesztés, nyolcad-pontok érintőivel
     •     Kör, négyzet, érintők, alkotók árnyéka


14. ábra: Henger felső karimájának a palást belsejébe vetett árnyéka.


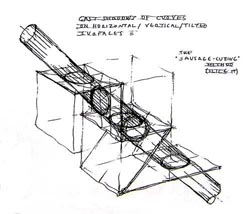
15. ábra: Ívek árnyéka vízszintes, függőleges és ferde síkokon - a "szalámi-szeletelés" módszere.


16. ábra: A fény-henger vízszintes, függőleges ill. ferde síkú metszetei megannyi, eredeti tömegből származó ellipszist eredményez.



FELADATOK


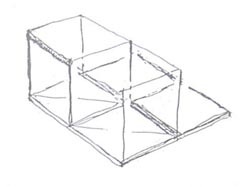
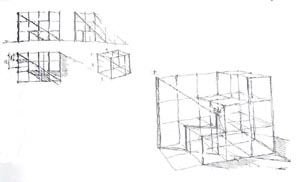
1 - Oszlop árnyéka (kockákkal modellezett) lépcsősoron

17. ábra: Oszlop árnyéka lépcsőn - perspektíva és vetületek.


2 - Létra árnyéka kocka-halmon

18. ábra: Létra árnyéka lépcsőzetes tömegen - perspektíva és vetületek.


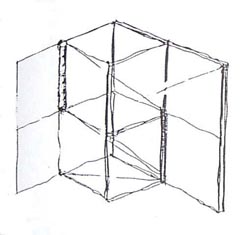
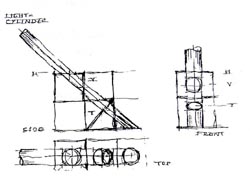
3 - Felső ablaksor fénycsíkja belső térben

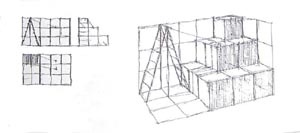
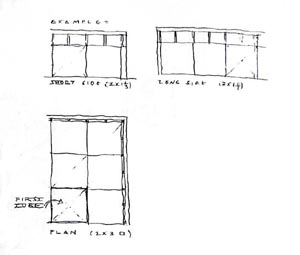
19. ábra: Falnézetek és alaprajz, befoglaló négyzethálóval (A belső tér aránya legyen pl. 2 x 3 x 1/3 egység).




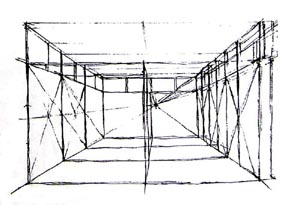
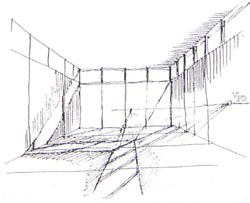
20. ábra: A csarnok - belső távlati képe


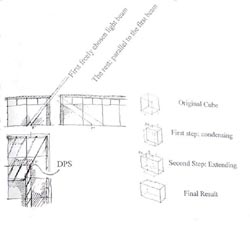
21. ábra: A megoldás lépései: fokozatosan téglatestté alakul a fénysugár befoglaló kockája. Meghatározónak tűnik az ablak-csík sarok-osztásának alsó pontja (P). Perspektívában most kijelöljük a kívánt árnyék pontját (PDS) a padlón. Ezt visszük át a többi vetületi rajzra i -, megfelelően összenyomva ill. kiterjesztve az eredeti befoglaló kockát. Végül P és DPS összekötésével eljutunk a térátlóként szereplő fő fénysugárhoz.

     •     Az eredeti kocka...
     •     Először: zsugorítjuk...
     •     Másodszor: kitágítjuk a befoglaló fény-dobozt.
     •     Íme a megfelelő arányban módosított befoglaló
           hasáb!

DPS = a kívánt árnyékpont (Desired Point of Shadow)


22. ábra: A távlati kép keresett fénycsíkja.

VPD = Átlók iránypontja (Vanishing Point of Diagonals)



ÖSSZEFOGLALÁS


     Kezdetben feltételezhetjük, hogy a fő fénysugár pontosan egybeesik egy kocka térátlójával Ezt a fénysugár értelmezésére kitalált befoglaló kockát "fény-doboznak" nevezzük.
     A kívánt árnyékpontot összekötve az árnyékvető ponttal, perspektívában meghatározzuk a fénysugár valós irányát. Ezután a vetületi rajzokon is tisztázzuk a módosított befoglaló fénydoboz végleges arányait.
     A fény-sík és az árnyék-felfogó felület metszésvonalait (azaz a vetett árnyékot) először a vetületeken keressük meg.
 
 
*Először angolul jelent meg ("Cast Shadow Construction" UIUC, 2001).
 
 

 © Minden jog fenntartva. Dr. Méhes Balázs PhD egyetemi docens
ajánlott felbontás 1024×768